Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
7. Systems of Equations & Matrices
Determinants and Cramer's Rule
Problem 27a
Textbook Question
Evaluate each determinant. See Example 3.
 Verified step by step guidance
Verified step by step guidance1
Identify the size of the matrix. If it's a 2x2 matrix, use the formula for the determinant: \( \text{det}(A) = ad - bc \) for a matrix \( A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \).
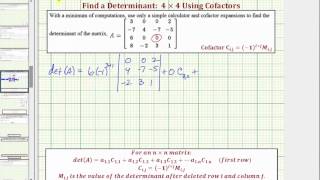
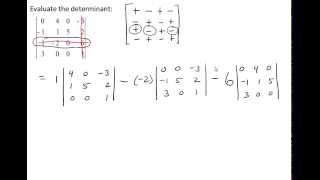
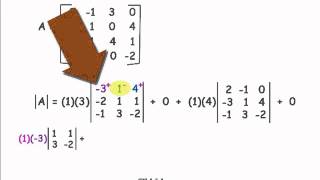
If the matrix is larger than 2x2, use cofactor expansion to evaluate the determinant. Choose a row or column to expand along, typically the one with the most zeros to simplify calculations.
For each element in the chosen row or column, calculate the minor by removing the row and column of that element, then find the determinant of the resulting smaller matrix.
Multiply each minor by its corresponding cofactor, which is \((-1)^{i+j}\) times the minor, where \(i\) and \(j\) are the row and column indices of the element.
Sum all the products of elements and their cofactors to find the determinant of the original matrix.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Determinants
A determinant is a scalar value that can be computed from the elements of a square matrix. It provides important information about the matrix, such as whether it is invertible (non-zero determinant) or singular (zero determinant). Determinants can be calculated using various methods, including expansion by minors or row reduction.
Recommended video:
Guided course

Determinants of 2×2 Matrices
Matrix Operations
Matrix operations, including addition, subtraction, and multiplication, are fundamental in linear algebra. Understanding how to manipulate matrices is essential for evaluating determinants, as the properties of matrices directly affect their determinants. For example, the determinant of a product of matrices equals the product of their determinants.
Recommended video:
Guided course

Performing Row Operations on Matrices
Cofactor Expansion
Cofactor expansion is a method used to calculate the determinant of a matrix by breaking it down into smaller matrices. This technique involves selecting a row or column, multiplying each element by its corresponding cofactor (which is the determinant of the submatrix formed by removing the row and column of that element), and summing these products. It is particularly useful for larger matrices.

 4:36m
4:36mWatch next
Master Determinants of 2×2 Matrices with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice