Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
3. Functions
Function Composition
Problem 25b
Textbook Question
Determine whether each function graphed or defined is one-to-one. y = x+4 / x-3
 Verified step by step guidance
Verified step by step guidance1
Understand that a function is one-to-one if each output value is paired with exactly one input value, meaning it passes the Horizontal Line Test.
Consider the function \( y = \frac{x+4}{x-3} \). This is a rational function, which can be analyzed for one-to-one properties.
To determine if the function is one-to-one, check if it passes the Horizontal Line Test. This involves ensuring that no horizontal line intersects the graph of the function more than once.
Alternatively, algebraically determine if the function is one-to-one by checking if \( f(a) = f(b) \) implies \( a = b \). Set \( \frac{a+4}{a-3} = \frac{b+4}{b-3} \) and solve for \( a = b \).
Simplify the equation \( (a+4)(b-3) = (b+4)(a-3) \) and see if it leads to \( a = b \) for all values in the domain of the function.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
One-to-One Function
A one-to-one function is a type of function where each output value is associated with exactly one input value. This means that no two different inputs produce the same output. To determine if a function is one-to-one, one can use the horizontal line test: if any horizontal line intersects the graph of the function more than once, the function is not one-to-one.
Recommended video:

Decomposition of Functions
Graphing Rational Functions
Rational functions are expressed as the ratio of two polynomials. The function given, y = (x + 4) / (x - 3), is a rational function. Understanding how to graph rational functions involves identifying asymptotes, intercepts, and the general shape of the graph, which can help in visualizing whether the function is one-to-one.
Recommended video:
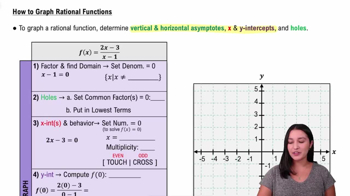
How to Graph Rational Functions
Asymptotes
Asymptotes are lines that a graph approaches but never touches. For the function y = (x + 4) / (x - 3), there is a vertical asymptote at x = 3, where the function is undefined. Recognizing asymptotes is crucial for understanding the behavior of the function and can influence whether the function is one-to-one, especially in the context of its range.
Recommended video:

Introduction to Asymptotes

 4:56m
4:56mWatch next
Master Function Composition with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice