Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
1. Equations & Inequalities
Linear Inequalities
Problem 15a
Textbook Question
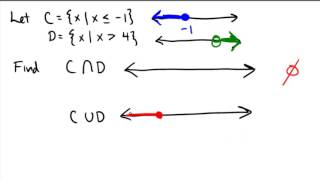
Textbook QuestionIn Exercises 15–26, use graphs to find each set. (- 3, 0) ∩ [- 1, 2]
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Intervals
An interval is a set of real numbers that fall between two endpoints. Intervals can be open, closed, or half-open. For example, the interval (-3, 0) is open, meaning it includes all numbers greater than -3 and less than 0, but not -3 and 0 themselves. The interval [-1, 2] is closed, including both endpoints -1 and 2.
Recommended video:

Interval Notation
Intersection of Sets
The intersection of two sets is the set of elements that are common to both sets. In this case, we are looking for the numbers that are present in both the interval (-3, 0) and the interval [-1, 2]. The intersection is found by identifying the overlapping values between the two intervals.
Recommended video:
Guided course

Parallel & Perpendicular Lines
Graphing Intervals
Graphing intervals involves representing the sets of numbers visually on a number line. Open intervals are shown with parentheses, while closed intervals are represented with brackets. This visual representation helps in easily identifying overlaps and intersections between different sets, making it easier to determine the solution to the problem.
Recommended video:

Identifying Intervals of Unknown Behavior
Related Videos
Related Practice