Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
3. Functions
Intro to Functions & Their Graphs
Problem 39d
Textbook Question
Graph each equation. 2x +5y = 20
 Verified step by step guidance
Verified step by step guidance1
Step 1: The given equation is in the standard form Ax + By = C. We need to convert it into slope-intercept form y = mx + b, where m is the slope and b is the y-intercept.
Step 2: To convert the equation into slope-intercept form, isolate y. Subtract 2x from both sides to get 5y = -2x + 20.
Step 3: Divide every term by 5 to solve for y. This gives y = -2/5x + 4.
Step 4: Now that we have the equation in slope-intercept form, we can identify the slope and y-intercept. The slope (m) is -2/5 and the y-intercept (b) is 4.
Step 5: To graph the equation, start by plotting the y-intercept (0,4) on the y-axis. Then, from this point, use the slope to find the next point. Since the slope is -2/5, go down 2 units and to the right 5 units. Plot this point and draw a line through the two points. This line represents the graph of the equation.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Linear Equations
A linear equation is an algebraic expression that represents a straight line when graphed on a coordinate plane. It typically takes the form Ax + By = C, where A, B, and C are constants. The solutions to a linear equation are the points (x, y) that satisfy the equation, and the graph of the equation shows all these solutions.
Recommended video:

Categorizing Linear Equations
Slope-Intercept Form
The slope-intercept form of a linear equation is given by y = mx + b, where m represents the slope of the line and b represents the y-intercept. This form is particularly useful for quickly identifying the slope and y-intercept, allowing for easier graphing. Converting a standard form equation, like 2x + 5y = 20, into slope-intercept form can simplify the graphing process.
Recommended video:
Guided course
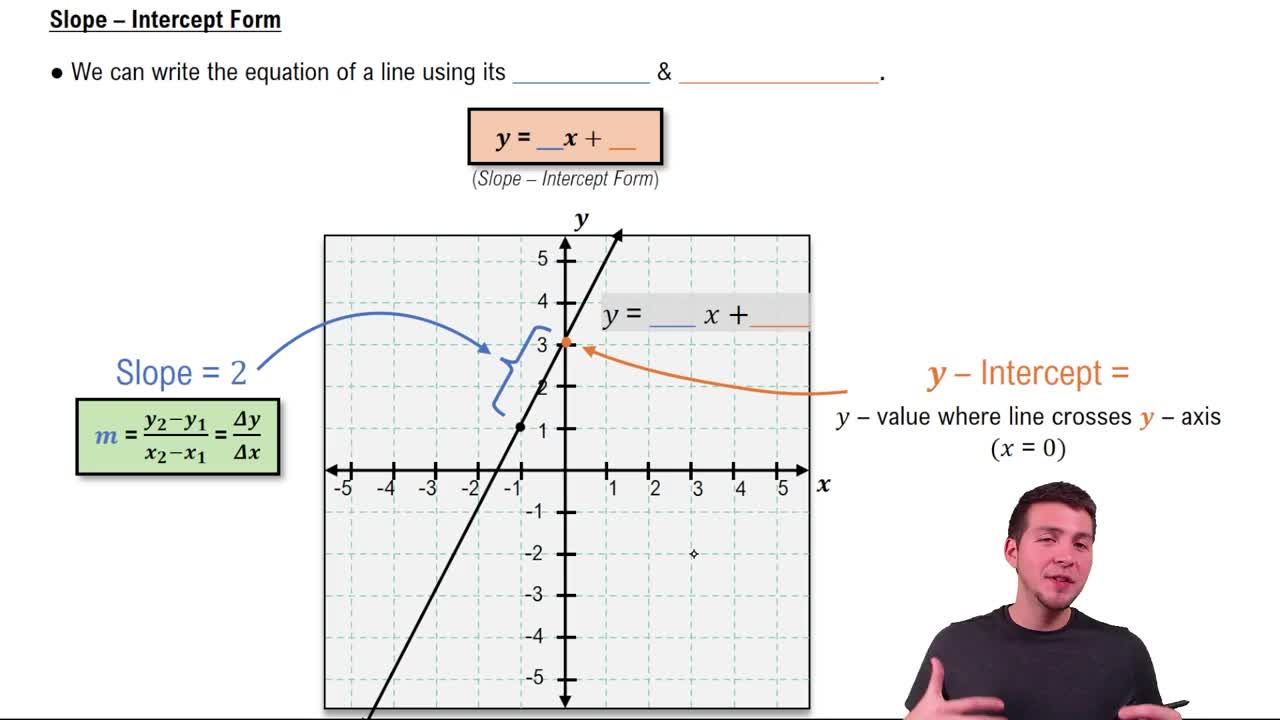
Slope-Intercept Form
Graphing Linear Equations
Graphing a linear equation involves plotting points that satisfy the equation on a coordinate plane and connecting them to form a straight line. To graph the equation 2x + 5y = 20, one can find the x-intercept and y-intercept or convert it to slope-intercept form. Understanding how to plot these points accurately is essential for visualizing the relationship between the variables.
Recommended video:

Categorizing Linear Equations

 5:2m
5:2mWatch next
Master Relations and Functions with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice






