Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
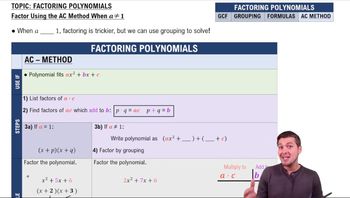
Factoring Polynomials
Problem 91b
Textbook Question
Textbook QuestionFactor each polynomial. See Example 7. m^4-3m^2-10
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Factoring Polynomials
Factoring polynomials involves rewriting a polynomial as a product of simpler polynomials or factors. This process is essential for solving polynomial equations and simplifying expressions. Common methods include factoring out the greatest common factor, using special products, and applying techniques like grouping or the quadratic formula when applicable.
Recommended video:
Guided course

Introduction to Factoring Polynomials
Quadratic Form
The expression m^4 - 3m^2 - 10 can be viewed as a quadratic in terms of m^2. By substituting m^2 with a new variable (e.g., x), the polynomial transforms into a standard quadratic form, making it easier to factor. Recognizing this structure allows for the application of quadratic factoring techniques, such as finding two numbers that multiply to the constant term and add to the linear coefficient.
Recommended video:

Vertex Form
Zero Product Property
The Zero Product Property states that if the product of two factors equals zero, at least one of the factors must be zero. This principle is crucial when solving polynomial equations after factoring, as it allows us to set each factor equal to zero to find the roots of the polynomial. Understanding this property is fundamental for solving equations and analyzing polynomial behavior.
Recommended video:

Product, Quotient, and Power Rules of Logs

 7:30m
7:30mWatch next
Master Introduction to Factoring Polynomials with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice