Here are the essential concepts you must grasp in order to answer the question correctly.
Continuity of Functions
A function is continuous at a point if the limit of the function as it approaches that point equals the function's value at that point. This means there are no breaks, jumps, or holes in the graph at that point. For a function to be continuous over an interval, it must be continuous at every point within that interval.
Recommended video:
Graphs of Common Functions
Types of Discontinuities
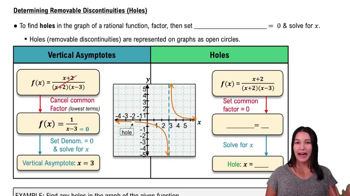
Discontinuities can be classified into three main types: removable, jump, and infinite. A removable discontinuity occurs when a function is not defined at a point but can be made continuous by defining it appropriately. A jump discontinuity occurs when the left-hand and right-hand limits exist but are not equal. An infinite discontinuity occurs when the function approaches infinity at a certain point.
Recommended video:
Determining Removable Discontinuities (Holes)
Interval Notation
Interval notation is a way of representing a range of values on the number line. It uses parentheses and brackets to indicate whether endpoints are included (closed interval) or excluded (open interval). For example, the interval (a, b) includes all numbers between a and b but not a and b themselves, while [a, b] includes a and b.
Recommended video:

 Verified Solution
Verified Solution


 5:2m
5:2m
