Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
2. Graphs of Equations
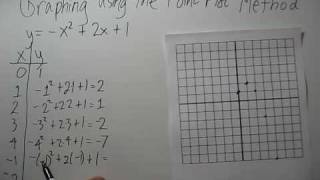
Two-Variable Equations
Problem 74
Textbook Question
Textbook QuestionIn Exercises 71–74, determine whether each statement is true or false. If the statement is false, make the necessary change(s) to produce a true statement. The ordered pair (2, 5) satisfies 3y - 2x = - 4.
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Ordered Pairs
An ordered pair consists of two elements, typically represented as (x, y), where 'x' is the first element and 'y' is the second. In the context of a coordinate plane, the first element indicates the horizontal position, while the second indicates the vertical position. Understanding ordered pairs is essential for evaluating whether they satisfy a given equation.
Recommended video:

Fundamental Counting Principle
Substitution in Equations
Substitution involves replacing variables in an equation with specific values to determine if the equation holds true. In this case, substituting the values from the ordered pair (2, 5) into the equation 3y - 2x = -4 allows us to check if the left-hand side equals the right-hand side. This process is fundamental in verifying the validity of statements involving equations.
Recommended video:
Guided course

Solving Systems of Equations - Substitution
Linear Equations
A linear equation is an equation that represents a straight line when graphed on a coordinate plane. It typically takes the form Ax + By = C, where A, B, and C are constants. Understanding the properties of linear equations, including how to manipulate and evaluate them, is crucial for determining the truth of statements involving specific points and their relationship to the equation.
Recommended video:

Categorizing Linear Equations

 5:28m
5:28mWatch next
Master Equations with Two Variables with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice