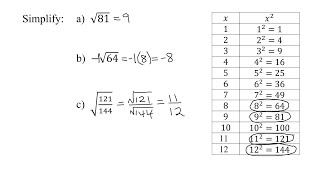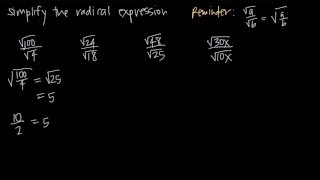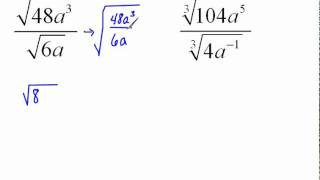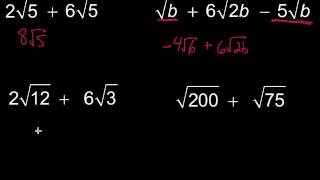In Exercises 1–20, evaluate each expression, or state that the expression is not a real number. ____ -√9/16

Key Concepts

Square Roots

A square root of a number 'x' is a value 'y' such that y² = x. For non-negative numbers, square roots yield real numbers, while negative numbers do not have real square roots. For example, √9 = 3, since 3² = 9, but √-1 is not a real number.

Negative Numbers and Real Numbers

Real numbers include all rational and irrational numbers, but they do not include imaginary numbers. When evaluating expressions involving square roots, if the radicand (the number under the square root) is negative, the result is not a real number. For instance, the square root of a negative number results in an imaginary number.

Fractional Expressions

A fractional expression is a ratio of two numbers, where the denominator is not zero. In the expression -√9/16, the numerator is the square root of 9, which is 3, and the denominator is 16. This results in a real number, specifically -3/16, since both components are real.