Here are the essential concepts you must grasp in order to answer the question correctly.
Inequalities
Inequalities are mathematical expressions that show the relationship between two values when they are not equal. They use symbols such as ≤ (less than or equal to), ≥ (greater than or equal to), < (less than), and > (greater than). Understanding how to interpret and manipulate inequalities is essential for solving problems that involve ranges of values rather than specific solutions.
Recommended video:
Graphing Linear Inequalities
Graphing linear inequalities involves representing the solutions of an inequality on a coordinate plane. The boundary line is drawn based on the corresponding equation, and the region that satisfies the inequality is shaded. For example, for the inequality x + 2y ≤ 6, the line x + 2y = 6 is drawn, and the area below this line is shaded to indicate all the points that satisfy the inequality.
Recommended video:
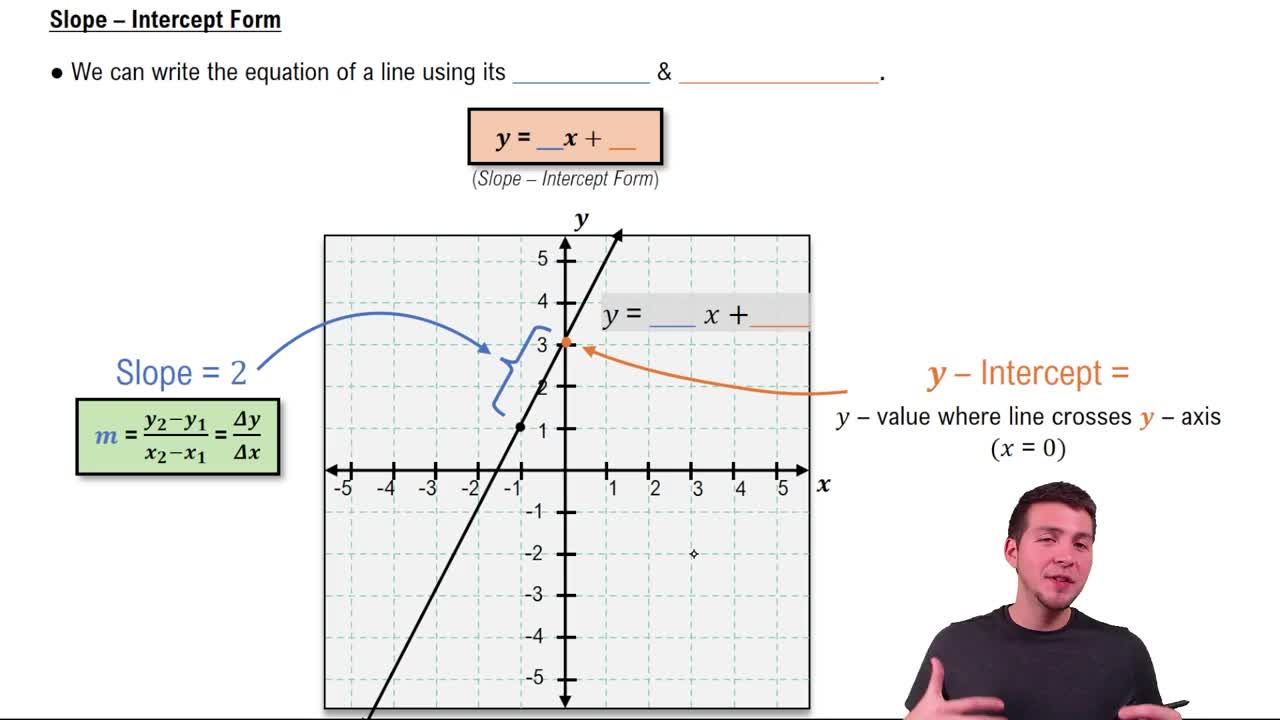
Slope-Intercept Form
The slope-intercept form of a linear equation is given by y = mx + b, where m represents the slope and b represents the y-intercept. This form is useful for quickly identifying how steep the line is and where it crosses the y-axis. Converting the inequality x + 2y ≤ 6 into slope-intercept form helps in graphing it accurately by determining the slope and intercept for the line.
Recommended video:
 Verified step by step guidance
Verified step by step guidance Verified Solution
Verified Solution


 7:2m
7:2m