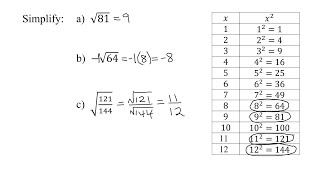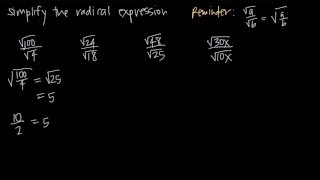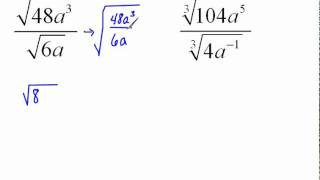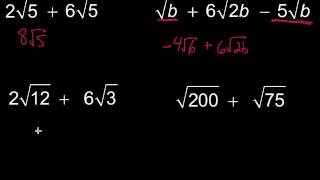Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
Radical Expressions
Problem 28b
Textbook Question
Textbook QuestionIn Exercises 1–38, solve each radical equation. (3x - 6)¹/³ + 5 = 8
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
6mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Radical Equations
Radical equations are equations that involve a variable within a radical, such as a square root or cube root. To solve these equations, one typically isolates the radical on one side and then raises both sides of the equation to the power that eliminates the radical. This process may introduce extraneous solutions, so it's important to check all potential solutions in the original equation.
Recommended video:
Guided course

Expanding Radicals
Isolating the Variable
Isolating the variable is a fundamental algebraic technique used to solve equations. This involves rearranging the equation to get the variable by itself on one side. In the context of radical equations, this often means moving constants or other terms away from the radical to simplify the equation before applying operations to eliminate the radical.
Recommended video:
Guided course

Equations with Two Variables
Extraneous Solutions
Extraneous solutions are solutions that emerge from the process of solving an equation but do not satisfy the original equation. This is particularly common in radical equations, where squaring both sides or other operations can introduce solutions that are not valid. Therefore, it is crucial to substitute any found solutions back into the original equation to verify their validity.
Recommended video:

Categorizing Linear Equations
Related Videos
Related Practice