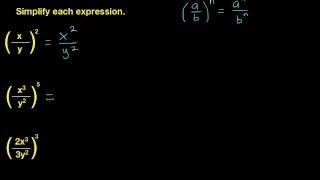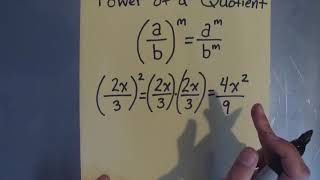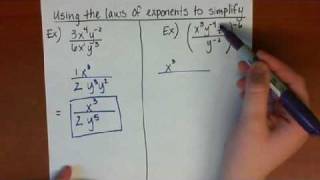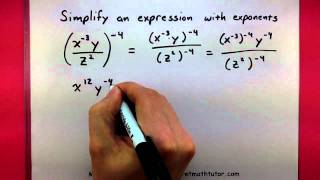Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
Exponents
Problem 77b
Textbook Question
In Exercises 75–84, state the name of the property illustrated. 6+(2+7)=(6+2)+7
 Verified step by step guidance
Verified step by step guidance1
Identify the operation involved in the expression: addition.
Observe the grouping of numbers in the expression: (6 + (2 + 7)) and ((6 + 2) + 7).
Notice that the order of the numbers does not change, only the grouping changes.
Recognize that this is an example of the Associative Property of Addition.
The Associative Property of Addition states that the way in which numbers are grouped in an addition problem does not change their sum.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Associative Property of Addition
The Associative Property of Addition states that the way in which numbers are grouped in an addition operation does not affect the sum. This means that for any numbers a, b, and c, the equation (a + b) + c = a + (b + c) holds true. In the given example, 6 + (2 + 7) = (6 + 2) + 7 demonstrates this property by showing that regardless of how the numbers are grouped, the result remains the same.
Recommended video:

Change of Base Property
Commutative Property of Addition
The Commutative Property of Addition indicates that the order in which two numbers are added does not change the sum. For any numbers a and b, the equation a + b = b + a is valid. While the example provided does not directly illustrate this property, understanding it is essential for grasping the broader context of addition properties in algebra.
Recommended video:

Change of Base Property
Properties of Operations
Properties of operations are fundamental rules that govern how mathematical operations behave. In addition, the two primary properties are the Associative and Commutative properties. Recognizing these properties helps simplify expressions and solve equations more efficiently, as they provide flexibility in how numbers can be combined.
Recommended video:

Change of Base Property

 7:39m
7:39mWatch next
Master Introduction to Exponent Rules with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice