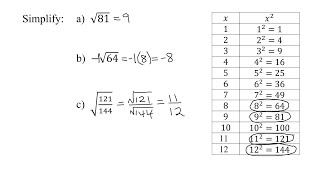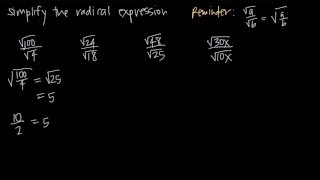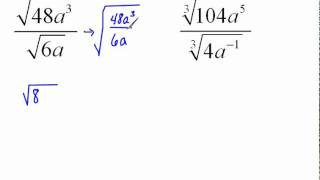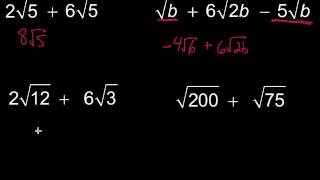Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
Radical Expressions
Problem 123a
Textbook Question
Textbook Question___ The domain of f(x) = ³√x−4 is [4, ∞).
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Domain of a Function
The domain of a function refers to the set of all possible input values (x-values) for which the function is defined. For the function f(x) = ³√x−4, the domain is determined by the values of x that do not lead to undefined expressions. In this case, since the cube root function is defined for all real numbers, the domain starts from 4 and extends to positive infinity.
Recommended video:

Domain Restrictions of Composed Functions
Cube Root Function
The cube root function, denoted as ³√x, is the inverse operation of cubing a number. It takes a real number x and returns a value y such that y³ = x. Unlike square roots, cube roots can accept negative values, which means they are defined for all real numbers. This property is crucial in determining the domain of the function f(x) = ³√x−4.
Recommended video:

Imaginary Roots with the Square Root Property
Vertical Shift
A vertical shift occurs when a constant is added or subtracted from a function, affecting its output values without altering its input values. In the function f(x) = ³√x−4, the '-4' indicates a downward shift of the cube root function by 4 units. This shift does not impact the domain but changes the range of the function, which is important for understanding its overall behavior.
Recommended video:

Shifts of Functions
Related Videos
Related Practice