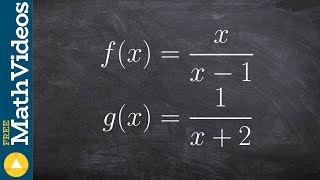In Exercises 1–30, find the domain of each function. f(x) = √(24 - 2x)

Key Concepts

Domain of a Function

The domain of a function refers to the set of all possible input values (x-values) for which the function is defined. For real-valued functions, this often involves identifying restrictions based on the operations involved, such as division by zero or taking square roots of negative numbers.

Square Root Function

A square root function, denoted as √(x), is defined only for non-negative values of x. This means that the expression inside the square root must be greater than or equal to zero to yield real number outputs. Understanding this is crucial for determining the domain of functions involving square roots.

Inequalities

Inequalities are mathematical expressions that show the relationship between two values, indicating that one is greater than, less than, or equal to the other. In the context of finding the domain, solving inequalities helps identify the range of x-values that satisfy the conditions imposed by the function, such as ensuring the expression under a square root is non-negative.