Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
4. Polynomial Functions
Understanding Polynomial Functions
Problem 58a
Textbook Question
Show that the real zeros of each polynomial function satisfy the given conditions. See Example 6. ƒ(x)=2x^5-x^4+2x^3-2x^2+4x-4; no real zero greater than 1
 Verified step by step guidance
Verified step by step guidance1
<Step 1: Understand the problem.> We need to show that the real zeros of the polynomial function \( f(x) = 2x^5 - x^4 + 2x^3 - 2x^2 + 4x - 4 \) satisfy the condition that there is no real zero greater than 1.
<Step 2: Use the Rational Root Theorem.> The Rational Root Theorem suggests that any rational root, in the form of \( \frac{p}{q} \), where \( p \) is a factor of the constant term (-4) and \( q \) is a factor of the leading coefficient (2), could be a potential zero. List these possible rational roots.
<Step 3: Test potential rational roots.> Substitute each potential rational root into the polynomial \( f(x) \) to check if it results in zero. This will help identify any real zeros.
<Step 4: Apply Descartes' Rule of Signs.> Use Descartes' Rule of Signs to determine the number of positive real roots. Count the number of sign changes in \( f(x) \) to estimate the number of positive real roots.
<Step 5: Analyze the results.> Based on the results from testing potential rational roots and applying Descartes' Rule of Signs, conclude whether there are any real zeros greater than 1. If none of the tested roots greater than 1 are zeros, the condition is satisfied.>
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
6mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Polynomial Functions
A polynomial function is a mathematical expression involving a sum of powers in one or more variables multiplied by coefficients. The general form is f(x) = a_n*x^n + a_(n-1)*x^(n-1) + ... + a_1*x + a_0, where 'n' is a non-negative integer and 'a_n' are constants. Understanding the behavior of polynomial functions, including their degree and leading coefficient, is essential for analyzing their zeros.
Recommended video:

Introduction to Polynomial Functions
Real Zeros
Real zeros of a polynomial function are the values of 'x' for which the function evaluates to zero. These points are crucial for understanding the function's graph, as they indicate where the graph intersects the x-axis. The Fundamental Theorem of Algebra states that a polynomial of degree 'n' has exactly 'n' roots, counting multiplicities, which can be real or complex.
Recommended video:

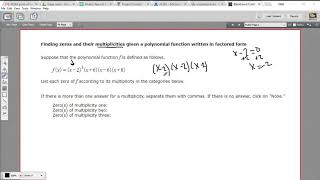
Finding Zeros & Their Multiplicity
Behavior of Polynomials at Infinity
The behavior of polynomial functions as 'x' approaches positive or negative infinity is determined by the leading term of the polynomial. For example, if the leading term is positive and of odd degree, the function will approach positive infinity as 'x' approaches positive infinity and negative infinity as 'x' approaches negative infinity. This behavior helps in determining the number of real zeros and their possible locations, particularly in relation to given conditions like 'no real zero greater than 1.'
Recommended video:

End Behavior of Polynomial Functions

 6:04m
6:04mWatch next
Master Introduction to Polynomial Functions with a bite sized video explanation from Callie
Start learningRelated Videos
Related Practice