Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
7. Systems of Equations & Matrices
Determinants and Cramer's Rule
Problem 25d
Textbook Question
Textbook QuestionFind the inverse, if it exists, for each matrix. [3x3 matrix]
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
9mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Matrix Inversion
Matrix inversion is the process of finding a matrix that, when multiplied with the original matrix, yields the identity matrix. For a square matrix A, the inverse is denoted as A⁻¹, and it exists only if the matrix is non-singular, meaning its determinant is non-zero. The inverse is crucial in solving systems of linear equations and in various applications across mathematics and engineering.
Recommended video:

Graphing Logarithmic Functions
Determinant
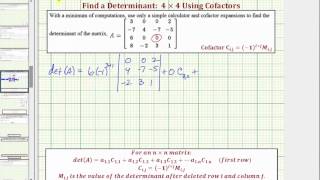
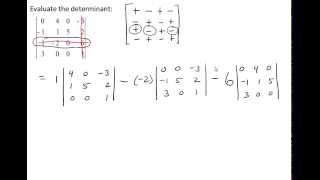
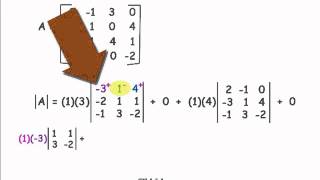
The determinant is a scalar value that provides important information about a square matrix, including whether it is invertible. For a 3x3 matrix, the determinant can be calculated using a specific formula involving the elements of the matrix. If the determinant is zero, the matrix is singular and does not have an inverse; if it is non-zero, the matrix is invertible.
Recommended video:
Guided course

Determinants of 2×2 Matrices
Adjugate Matrix
The adjugate matrix, or adjoint, is a matrix derived from the original matrix that is used in the calculation of the inverse. For a 3x3 matrix, the adjugate is formed by taking the transpose of the cofactor matrix. The inverse of a matrix can be computed using the formula A⁻¹ = (1/det(A)) * adj(A), where det(A) is the determinant and adj(A) is the adjugate matrix.
Recommended video:
Guided course

Introduction to Matrices

 4:36m
4:36mWatch next
Master Determinants of 2×2 Matrices with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice