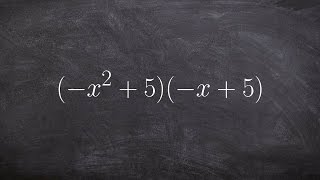Identify each expression as a polynomial or not a polynomial. For each polynomial, give the degree and identify it as a monomial, binomial, trinomial, or none of these.See Example 1. 5

Key Concepts

Polynomial Definition

A polynomial is a mathematical expression consisting of variables raised to non-negative integer powers and coefficients. It can include constants and can be expressed in the form of a sum of terms, where each term is a product of a coefficient and a variable raised to a power. Examples include expressions like 3x^2 + 2x + 1, which is a polynomial, and 4/x, which is not.

Degree of a Polynomial

The degree of a polynomial is the highest power of the variable in the expression. It provides insight into the polynomial's behavior and shape when graphed. For instance, in the polynomial 2x^3 + 5x^2 - x + 7, the degree is 3, indicating that the term with the highest exponent dominates the polynomial's behavior as x approaches infinity.

Classification of Polynomials

Polynomials can be classified based on the number of terms they contain. A monomial has one term (e.g., 4x), a binomial has two terms (e.g., x^2 + 3), and a trinomial has three terms (e.g., x^2 + 2x + 1). If a polynomial has more than three terms, it is typically referred to as 'none of these' in classification terms.