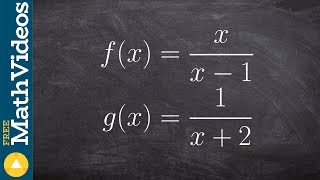Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
3. Functions
Function Composition
Problem 13c
Textbook Question
Determine whether each function graphed or defined is one-to-one. 
 Verified step by step guidance
Verified step by step guidance1
Identify the function type: The graph shown is a parabola, which is a quadratic function.
Understand the definition of a one-to-one function: A function is one-to-one if and only if every horizontal line intersects the graph of the function at most once.
Apply the Horizontal Line Test: Draw horizontal lines across the graph. If any horizontal line intersects the graph more than once, the function is not one-to-one.
Analyze the intersections: Observe that horizontal lines intersect the parabola at two points in most cases.
Conclude: Since horizontal lines intersect the graph at more than one point, the function is not one-to-one.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
One-to-One Function
A function is considered one-to-one if each output value corresponds to exactly one input value. This means that no two different inputs can produce the same output. To determine if a function is one-to-one, one can use the horizontal line test: if any horizontal line intersects the graph of the function more than once, the function is not one-to-one.
Recommended video:

Decomposition of Functions
Horizontal Line Test
The horizontal line test is a visual method used to determine if a function is one-to-one. If a horizontal line drawn across the graph intersects the curve at more than one point, the function fails the test and is not one-to-one. This test is particularly useful for analyzing the graphs of functions, such as parabolas, to quickly assess their one-to-one nature.
Recommended video:
Guided course

The Slope of a Line
Quadratic Functions
Quadratic functions are polynomial functions of degree two, typically expressed in the form f(x) = ax² + bx + c, where a, b, and c are constants and a ≠ 0. The graph of a quadratic function is a parabola, which can open upwards or downwards. Since parabolas are symmetric, they often fail the horizontal line test, indicating that they are not one-to-one functions.
Recommended video:

Solving Quadratic Equations Using The Quadratic Formula

 4:56m
4:56mWatch next
Master Function Composition with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice