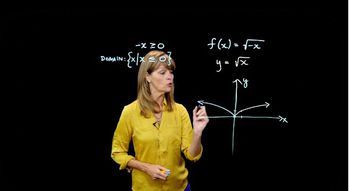Graph each function. See Examples 6–8 and the Summary of Graphing Techniques box following Example 9. ƒ(x)=2√x+1

Key Concepts

Function Definition

A function is a relation that assigns exactly one output for each input from its domain. In the case of ƒ(x) = 2√x + 1, the function takes a non-negative input x, applies the square root, scales it by 2, and then shifts the result up by 1. Understanding the definition of a function is crucial for graphing, as it helps identify the relationship between x and ƒ(x).

Graphing Techniques

Graphing techniques involve methods for visually representing functions on a coordinate plane. This includes identifying key features such as intercepts, asymptotes, and the overall shape of the graph. For the function ƒ(x) = 2√x + 1, recognizing that it is a transformation of the basic square root function will aid in accurately plotting its graph.

Transformations of Functions

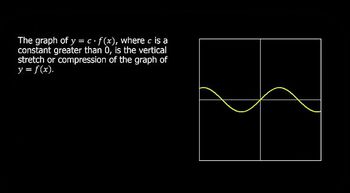
Transformations of functions refer to changes made to the basic form of a function that affect its graph. These can include vertical shifts, horizontal shifts, stretches, and compressions. In ƒ(x) = 2√x + 1, the factor of 2 indicates a vertical stretch, while the +1 indicates a vertical shift upwards, both of which are essential for accurately graphing the function.