Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
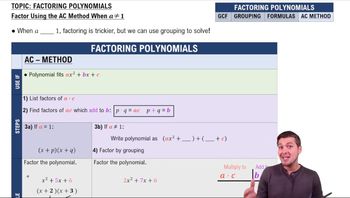
Factoring Polynomials
Problem 7c
Textbook Question
In Exercises 1–22, factor the greatest common factor from each polynomial. 12x⁴ − 8x²
 Verified step by step guidance
Verified step by step guidance1
Identify the greatest common factor (GCF) of the coefficients and the variables in the polynomial. Here, the coefficients are 12 and 8, and the variables are $x^4$ and $x^2$.
Find the GCF of the coefficients 12 and 8. The GCF is 4.
Determine the GCF of the variable terms $x^4$ and $x^2$. The GCF is $x^2$ because it is the highest power of $x$ that divides both terms.
Combine the GCFs of the coefficients and the variables to get the overall GCF, which is $4x^2$.
Factor out the GCF $4x^2$ from the polynomial $12x^4 - 8x^2$ by dividing each term by $4x^2$ and expressing the polynomial as a product of the GCF and the resulting polynomial.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Greatest Common Factor (GCF)
The Greatest Common Factor (GCF) is the largest factor that divides two or more numbers or terms without leaving a remainder. In polynomials, the GCF is determined by identifying the highest power of each variable and the largest coefficient common to all terms. Factoring out the GCF simplifies the polynomial and makes further operations easier.
Recommended video:

Graphs of Common Functions
Factoring Polynomials
Factoring polynomials involves rewriting a polynomial as a product of its factors. This process is essential for simplifying expressions, solving equations, and analyzing polynomial behavior. The first step in factoring is often to identify and extract the GCF, which can then lead to further factorization of the remaining polynomial.
Recommended video:
Guided course

Introduction to Factoring Polynomials
Polynomial Terms
Polynomial terms are the individual components of a polynomial, typically expressed in the form of ax^n, where 'a' is a coefficient, 'x' is a variable, and 'n' is a non-negative integer representing the degree of the term. Understanding the structure of polynomial terms is crucial for identifying the GCF and performing polynomial operations, as it allows for the recognition of common factors across the terms.
Recommended video:
Guided course

Introduction to Polynomials

 7:30m
7:30mWatch next
Master Introduction to Factoring Polynomials with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice