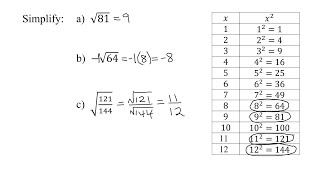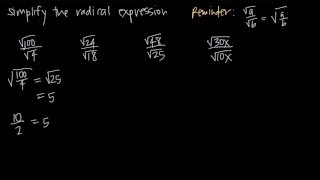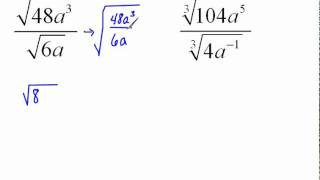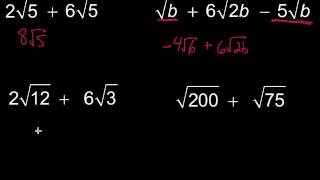Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
Radical Expressions
Problem 30b
Textbook Question
Textbook QuestionIn Exercises 1–38, solve each radical equation. (2x + 3)¹/⁴ + 7 = 10
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
6mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Radical Equations
Radical equations are equations that involve a variable within a radical (root) symbol. To solve these equations, one typically isolates the radical on one side and then raises both sides of the equation to the power that eliminates the radical. This process may need to be repeated if there are multiple radicals, and it's important to check for extraneous solutions that may arise from the manipulation.
Recommended video:
Guided course

Expanding Radicals
Isolating the Variable
Isolating the variable is a fundamental algebraic technique where one rearranges the equation to get the variable alone on one side. In the context of the given radical equation, this involves moving constants to the opposite side before applying operations to eliminate the radical. This step is crucial for simplifying the equation and making it easier to solve.
Recommended video:
Guided course

Equations with Two Variables
Extraneous Solutions
Extraneous solutions are solutions that emerge from the algebraic manipulation of an equation but do not satisfy the original equation. When solving radical equations, it is essential to check each potential solution by substituting it back into the original equation to ensure it holds true. This step helps to confirm the validity of the solutions obtained during the solving process.
Recommended video:

Categorizing Linear Equations
Related Videos
Related Practice