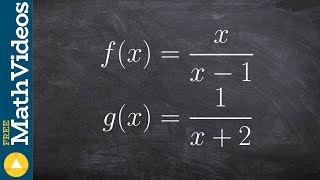Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
3. Functions
Function Composition
Problem 39b
Textbook Question
Textbook QuestionIn Exercises 31–50, find f−g and determine the domain for each function. f(x) = √x, g(x) = x − 4
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Function Operations
Function operations involve combining two functions to create a new function. In this case, f(x) and g(x) can be combined through subtraction to find f - g. Understanding how to perform operations on functions is essential for manipulating and analyzing their behavior.
Recommended video:

Multiplying & Dividing Functions
Domain of a Function
The domain of a function is the set of all possible input values (x-values) for which the function is defined. For f(x) = √x, the domain is x ≥ 0, since the square root of a negative number is not defined in the real number system. Identifying the domain is crucial when performing operations on functions to ensure the resulting function is valid.
Recommended video:

Domain Restrictions of Composed Functions
Composite Functions
Composite functions are formed when one function is applied to the result of another function. In this context, after finding f - g, it is important to analyze how the domains of f and g interact. Understanding composite functions helps in determining the overall domain of the resulting function after operations are performed.
Recommended video:

Function Composition

 4:56m
4:56mWatch next
Master Function Composition with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice