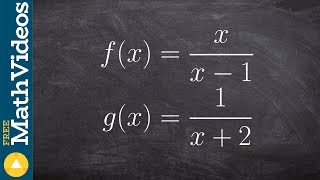Graph the inverse of each one-to-one function.

Verified step by step guidance

1. Identify the given function. The graph shows a linear function.
2. To find the inverse, swap the x and y coordinates of the function. This means reflecting the graph over the line y = x.
3. Determine the equation of the given line. It appears to be a linear function with a negative slope.
4. Solve the equation for y in terms of x to find the inverse function.
5. Graph the inverse function by plotting the new points and drawing the line that represents the inverse.

Key Concepts

One-to-One Functions

A one-to-one function is a type of function where each output value is paired with exactly one input value. This means that no two different inputs produce the same output. This property is crucial for determining whether a function has an inverse, as only one-to-one functions can be inverted without losing information.

Inverse Functions

An inverse function essentially reverses the effect of the original function. If a function f takes an input x and produces an output y, the inverse function f⁻¹ takes y as input and returns x. Graphically, the inverse of a function can be found by reflecting the graph of the original function across the line y = x.

Graphing Inverses

When graphing the inverse of a function, the key step is to switch the x and y coordinates of each point on the original graph. This reflection across the line y = x allows for a visual representation of the inverse. Understanding how to manipulate coordinates is essential for accurately graphing the inverse function.