Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
2. Graphs of Equations
Lines
Problem 79
Textbook Question
Textbook QuestionIn Exercises 79–80, find the value of y if the line through the two given points is to have the indicated slope. (3, y) and (1, 4), m = −3
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
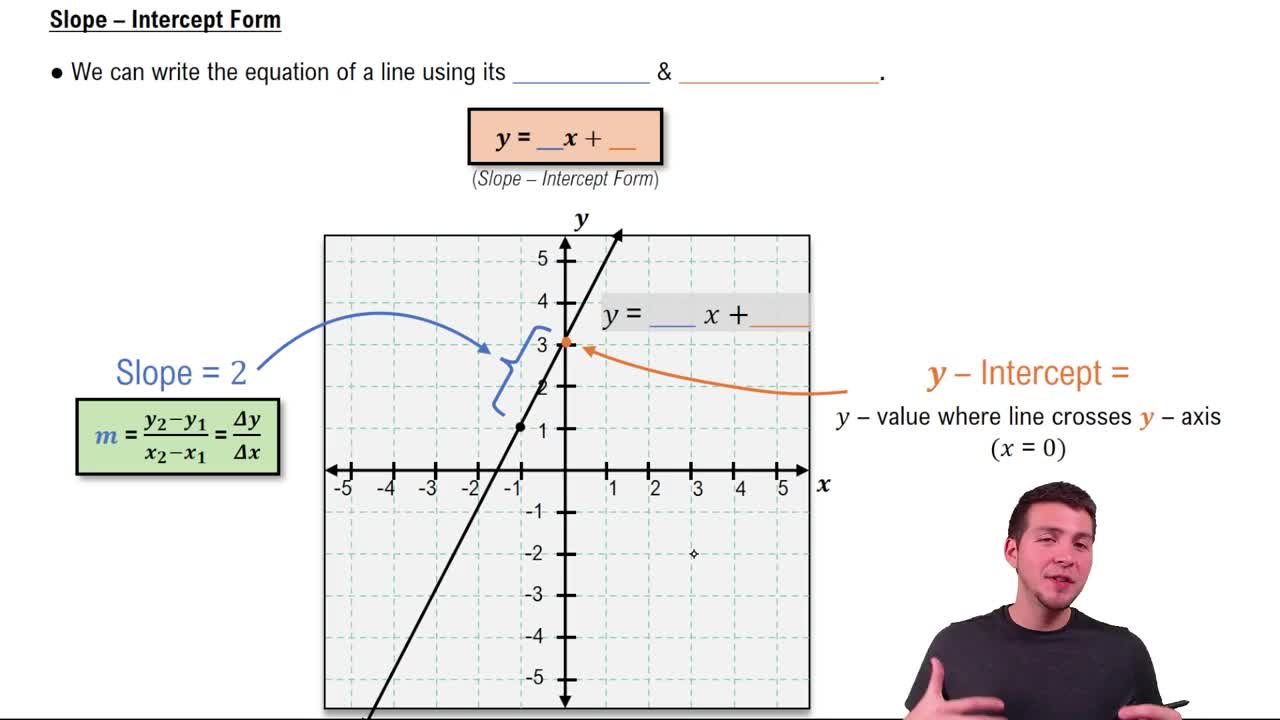
Slope of a Line
The slope of a line measures its steepness and direction, calculated as the change in the y-coordinates divided by the change in the x-coordinates between two points. In this case, the slope (m) is given as -3, indicating that for every unit increase in x, y decreases by 3 units.
Recommended video:
Guided course

The Slope of a Line
Point-Slope Form
The point-slope form of a linear equation is expressed as y - y1 = m(x - x1), where (x1, y1) is a point on the line and m is the slope. This form is particularly useful for finding the equation of a line when one point and the slope are known, allowing us to solve for unknown coordinates.
Recommended video:
Guided course

Point-Slope Form
Coordinate Geometry
Coordinate geometry involves the study of geometric figures using a coordinate system, typically the Cartesian plane. Understanding how to plot points, interpret coordinates, and apply formulas related to lines and slopes is essential for solving problems involving linear relationships between variables.
Recommended video:
Guided course

Graphs and Coordinates - Example

 6:49m
6:49mWatch next
Master The Slope of a Line with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice