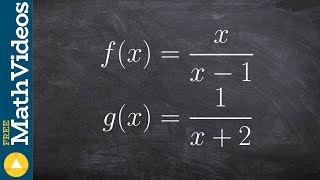Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
3. Functions
Function Composition
Problem 33d
Textbook Question
Textbook QuestionDetermine whether each function graphed or defined is one-to-one. y = ∛x+1 - 3
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
One-to-One Functions
A function is considered one-to-one if it assigns a unique output for every unique input, meaning no two different inputs produce the same output. This can be tested using the horizontal line test: if any horizontal line intersects the graph of the function more than once, the function is not one-to-one.
Recommended video:

Decomposition of Functions
Cubic Root Function
The cubic root function, represented as y = ∛x, is a type of radical function that returns the number which, when cubed, gives the input value x. This function is defined for all real numbers and is continuous and increasing, which contributes to its one-to-one nature.
Recommended video:

Imaginary Roots with the Square Root Property
Transformations of Functions
Transformations involve shifting, reflecting, stretching, or compressing the graph of a function. In the given function y = ∛x + 1 - 3, the transformations include a vertical shift of +1 and a downward shift of -3, which do not affect the one-to-one property of the original cubic root function.
Recommended video:

Domain & Range of Transformed Functions

 4:56m
4:56mWatch next
Master Function Composition with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice