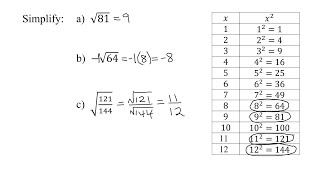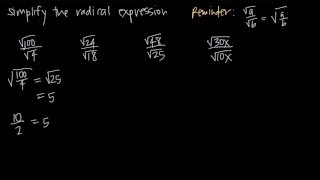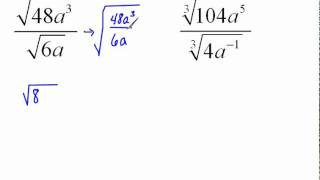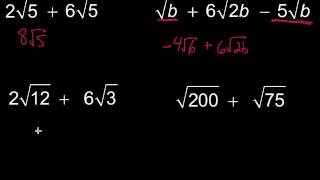Simplify each radical. Assume all variables represent positive real numbers. √192

Key Concepts

Radical Expressions

Radical expressions involve roots, such as square roots, cube roots, etc. The square root of a number 'x' is a value that, when multiplied by itself, gives 'x'. In this case, simplifying a radical means expressing it in its simplest form, often by factoring out perfect squares.

Perfect Squares

Perfect squares are numbers that can be expressed as the square of an integer. For example, 1, 4, 9, 16, and 25 are perfect squares. When simplifying radicals, identifying and factoring out perfect squares from the radicand (the number under the radical) helps in reducing the expression to its simplest form.

Properties of Square Roots

The properties of square roots include rules such as √(a*b) = √a * √b and √(a^2) = a. These properties allow for the manipulation and simplification of radical expressions. Understanding these properties is essential for breaking down complex radicals into simpler components, making the simplification process more manageable.