Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
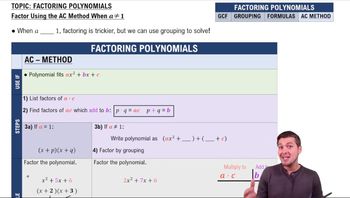
Factoring Polynomials
Problem 96d
Textbook Question
Textbook QuestionIn Exercises 91–100, find all values of x satisfying the given conditions. y = x^3 + 4x^2 - x + 6 and y = 10
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Polynomial Functions
A polynomial function is a mathematical expression involving a sum of powers in one or more variables multiplied by coefficients. In this case, the function y = x^3 + 4x^2 - x + 6 is a cubic polynomial, which means it has a degree of three. Understanding polynomial functions is essential for analyzing their behavior, including finding their roots or points of intersection with other functions.
Recommended video:

Introduction to Polynomial Functions
Finding Intersections
Finding intersections between two functions involves determining the points where their graphs meet. This is done by setting the two equations equal to each other. In this problem, we set the polynomial function equal to the constant value of 10, leading to the equation x^3 + 4x^2 - x + 6 = 10, which simplifies to finding the roots of a new polynomial.
Recommended video:

Finding the Domain of an Equation
Root Finding Techniques
Root finding techniques are methods used to determine the values of x for which a polynomial equals zero. Common methods include factoring, using the Rational Root Theorem, synthetic division, and numerical methods like the Newton-Raphson method. In this context, once the equation is simplified, applying these techniques will help identify the values of x that satisfy the original condition.
Recommended video:

Imaginary Roots with the Square Root Property

 7:30m
7:30mWatch next
Master Introduction to Factoring Polynomials with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice