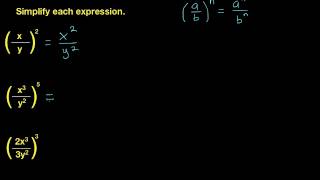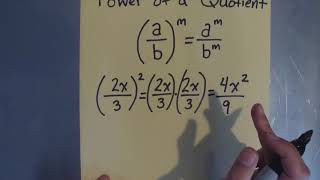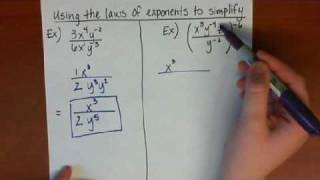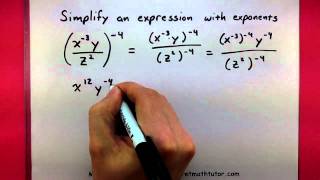Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
Exponents
Problem 16b
Textbook Question
Evaluate each expression. -|-12|
 Verified step by step guidance
Verified step by step guidance1
Understand that the expression involves the absolute value function, which is denoted by the vertical bars | |.
Recall that the absolute value of a number is its distance from zero on the number line, regardless of direction, meaning it is always non-negative.
Identify the number inside the absolute value bars, which in this case is -12.
Apply the absolute value function: |-12|, which means you take the positive value of -12.
Conclude that the absolute value of -12 is 12, as the absolute value function converts negative numbers to their positive counterparts.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Absolute Value
The absolute value of a number is its distance from zero on the number line, regardless of direction. It is denoted by vertical bars, such as |x|, and is always non-negative. For example, |3| equals 3, and |-3| also equals 3. Understanding absolute value is crucial for evaluating expressions that involve negative numbers.
Recommended video:

Parabolas as Conic Sections Example 1
Evaluating Expressions
Evaluating an expression involves substituting values for variables and performing the necessary arithmetic operations to simplify it. In this case, the expression |-12| requires recognizing that the absolute value function transforms negative inputs into positive outputs. Mastery of this concept is essential for solving various mathematical problems.
Recommended video:
Guided course

Evaluating Algebraic Expressions
Properties of Absolute Value
The properties of absolute value include the fact that |a| = a if a is non-negative, and |a| = -a if a is negative. Additionally, the absolute value of a product is the product of the absolute values, |ab| = |a||b|. These properties help in simplifying expressions and solving equations involving absolute values effectively.
Recommended video:

Change of Base Property

 7:39m
7:39mWatch next
Master Introduction to Exponent Rules with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice