Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
8. Conic Sections
Ellipses: Standard Form
Problem 1b
Textbook Question
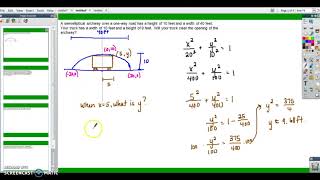
Textbook QuestionGraph the ellipse and locate the foci. (x^2)/36 +(y^2)/25 = 1
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Ellipse Definition
An ellipse is a set of points in a plane where the sum of the distances from two fixed points, called foci, is constant. The standard form of an ellipse's equation is (x^2/a^2) + (y^2/b^2) = 1, where 'a' and 'b' are the semi-major and semi-minor axes, respectively. In this case, the ellipse is centered at the origin with axes aligned to the coordinate axes.
Recommended video:

Foci and Vertices of an Ellipse
Graphing an Ellipse
To graph an ellipse, identify the lengths of the semi-major and semi-minor axes from the equation. For the given equation, a^2 = 36 (so a = 6) and b^2 = 25 (so b = 5). The ellipse will be elongated along the x-axis, with vertices at (±6, 0) and (0, ±5) on the y-axis, forming a closed curve.
Recommended video:

Graph Ellipses NOT at Origin
Foci of an Ellipse
The foci of an ellipse are located along the major axis, at a distance 'c' from the center, where c is calculated using the formula c = √(a^2 - b^2). For this ellipse, a = 6 and b = 5, so c = √(36 - 25) = √11. Thus, the foci are located at (±√11, 0), which are approximately (±3.32, 0).
Recommended video:

Foci and Vertices of an Ellipse

 5:12m
5:12mWatch next
Master Graph Ellipses at Origin with a bite sized video explanation from Nick Kaneko
Start learning