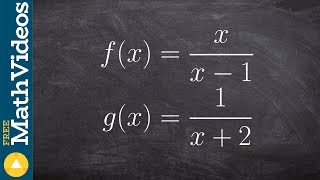In Exercises 1–30, find the domain of each function. f(x)=-2(x+5)

Verified step by step guidance

1. Identify the type of function given. The function \( f(x) = -2(x+5) \) is a linear function.
2. Recall that the domain of a linear function is all real numbers, because there are no restrictions such as division by zero or square roots of negative numbers.
3. Express the domain in interval notation. Since the domain is all real numbers, it can be written as \((-\infty, \infty)\).
4. Alternatively, express the domain in set notation. The domain can be written as \( \{ x \mid x \in \mathbb{R} \} \).
5. Conclude that the domain of the function \( f(x) = -2(x+5) \) is all real numbers.

Key Concepts

Domain of a Function

The domain of a function refers to the set of all possible input values (x-values) for which the function is defined. For polynomial functions like f(x) = -2(x + 5), the domain typically includes all real numbers, as there are no restrictions such as division by zero or square roots of negative numbers.

Polynomial Functions

Polynomial functions are mathematical expressions that involve variables raised to whole number powers, combined using addition, subtraction, and multiplication. The function f(x) = -2(x + 5) is a linear polynomial, which is a specific type of polynomial of degree one, indicating that it is defined for all real numbers.

Graphing Linear Functions

Graphing linear functions involves plotting points that satisfy the function's equation and connecting them to form a straight line. The function f(x) = -2(x + 5) can be rewritten in slope-intercept form, y = mx + b, which helps in identifying its slope and y-intercept, further confirming that its domain is all real numbers.