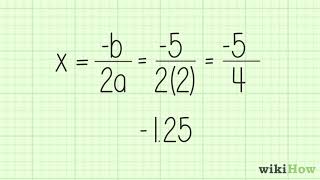Hi, my name is Rebecca Muller. Now, you should already be familiar with solving linear and quadratic equations, and in the previous session, we looked at linear functions. We're now going to go up one degree and look at quadratic functions. Those are also known as second degree functions. Here's a formal definition. A quadratic function is a function of the form f of x equals ax squared plus bx plus c, where a, b, and c are real numbers and our a value does not equal 0. So just like we had looked at quadratic equations where we had ax squared plus bx plus c equals 0. Now we're going to look at the two variable format where it's equal to f of x, a function of x. In specifics, let's look at our subtopics. We'll look at properties of a quadratic function, namely, we'll look at domain and range, and then we'll have the parabolic shape of the graph. We will consider the axis of symmetry for a quadratic function. We'll look at its intercepts and its vertex. We'll also look at methods for finding the vertex, and finally we'll look at optimization problems. So the most basic quadratic function is going to have the equation y equals x squared, or f of x equals x squared. Now, you may be familiar with this graph from having seen it in a previous section. We're going to do a little bit more detailed look at that graph now. In particular, if I just draw in a quick xy plane, and I'm going to just plot some points, so making a T-chart. Let's just plot values where x goes from negative to positive 3 along integer values. So squaring all of our x values will give us our y-coordinates. So negative 3 squared is the same as negative 3 times negative 3, which is going to give us a positive 9. Negative 2 times itself will end up giving us a value of 4. Negative 1 squared is 1, 0 squared is 0, 1 squared is 1, 2 squared is 4, 3 squared is 9. So now we need to plot these points. So on the xy plane, let's just start at the origin of plot 00. Then moving over one unit and then up one unit, I have the 0.1 comma 1. And then go over two units and go up to 2, 3, 4. I have the 0.2 comma 4. Let's kind of line it up here. And then moving over three, we need to go up to 9. So this is 5, 6, 7, 8, 9. And lining it up, that looks about right. Somewhere in there. When I look at my negative values for x, when I went to x equals to negative 1, I ended up at 1. When x was equal to negative 2, I ended up with four. When x was equal to negative 3, I ended up with 9. So again, kind of going up and about right there. Now we're going to connect the dots and assume that we have a general smooth shape between them. And in doing so, notice that this section down by the origin, we're going to round it off like this and then go up toward the right. And then as we move to the left, notice we have the same kind of shapes going on. So we end up with what is the characteristic shape of a quadratic function. It's going to be a U-shaped shaped graph, and that has a particular term that's associated with it-- it's called a parabola. Now, if you end up having conic sections somewhere in your future, you'll end up with a more geometric definition for what a parabola is. For now, we're just going to go with "a parabola is a U-shaped graph." Notice that in this parabola, we have a couple of things that we can point out. One is even from just using these values, you notice that when we substituted in the value of x, we came up with some f of x, but when we substituted in the value of negative x somewhere over here, we also came up with the value of f of x-- that is, f of negative x was actually the same value as f of x. So we had f of negative x was equal to f of x. That is, the y values are the same. When that occurs, we end up having a symmetry to the y-axis. So this is symmetric to our y-axis, which means that we have this line of symmetry that's going directly in between the two halves-- the two symmetric halves-- and that's going to be called our axis of symmetry. And so our axis of symmetry in this case is going to be the y-axis, whose equation is going to be x equals 0. So we end up with an axis of symmetry, and that equation is x equals 0. Remember that when you're talking about an axis, you're talking about a straight line. So don't just say that your axis of symmetry is 0. You need to give the equation of the line for that. Some other things to point out are that we end up having a domain of all real numbers, because we can square any number we'd like to. So our domain is going to be from negative infinity to positive infinity. And we have a range of values in this case, which is going to be only the non-negative values. Now, that's true for the y equals x squared, but in general, if we want to think about any parabola, notice that this point, which is in this case at the origin, is going to be that point that's going to lie along the axis of symmetry. Also notice that it's the lowest point in this graph, so picking up the y-coordinate of that lowest point, which is going to be a 0, and including it, and then saying we go all the way to infinity, gives us the range for this particular function. But in general, finding that point, which is going to be either the lowest point on the graph or-- had it been reflected-- the highest point on the graph, is going to give us a value that we're going to use in our range. That particular point, the minimum or the maximum value of the graph, is going to have a name, and that point is going to be called the vertex of that parabola. And so in our case, our vertex is at the origin, 0 comma 0. Now we're going to look at a few more examples where we're going to play off of this basic shape. Now, earlier in this course, you've probably looked at transformations already, and that included transformations of the squaring function. So let's see if you can remember some of the things that you've learned earlier, and I'm going to give you a chance to try that on this problem. What I'd like you to do is to look at the following function, which is f of x equals negative the quantity x plus squared plus 4, and I'd like to consider some things like, what does the graph look like? Can I think about it in terms of transformations? Which way would it be shifted or reflected or whatever else could be going on transformation-wise? Can you recall how to find intercepts for this graph, and then can you identify the domain and the range? So give yourself a few moments to see what it is you already remember, and then come back and we'll do it together. So let's look at what we know about transformations in working with this problem. We see that f of x equals. We have the negative there, which you'll recall means a reflection. Because the negative is taking place after we do the squaring, this is going to be a reflection across the x-axis. Then we notice that inside the parentheses, we have an addition of 2, and that's affecting our x value directly. So when that occurs, remember we take the opposite sign-- that is, we're going to think about this addition of as a shift and that shift is going to be impacting it horizontally. So which direction will we go? Well, it's x minus a negative 2, so therefore we're going to shift left two units. Then we notice the plus 4 here at the end. The plus 4 is occurring after you've already performed the function of squaring. So this is going to be a shift also, but this is going to be a shift up of four units. So if you've gone through transformations already, you should be able to identify that. So quickly thinking about what this is going to look like, it's going to be that x squared graph that's been shifted left two units and then up four units, and it's going to have been reflected. So a really quick sketch just to get a general idea and then we'll do a few more specifics. We would shift left two units and then up four units, and we'd have our vertex of our U-shape graph right here, and we know that this is going to be a parabola that's going to be opening downward. Now, I haven't found the intercepts yet, so don't rely on this as being exact. But we do at least have an idea of what's going on. We can now go a little bit more in detail and because we've solved quadratic equations before, we can find intercepts, like the x-intercepts in particular. Our y-intercept, of course, is fairly easy to find. We've used the value of x equal to 0, and substitute in a to find f of 0. That's going to equal a negative of. In parentheses we'd have 2 value squared, and then plus 4, and this is going to be a negative of 2 squared, so that's negative 4 plus 4, and that gives us a y-coordinate of 0. So actually, I could go back over here and kind of make that a big old dot, and we could see it goes to the origin. To find the x-intercepts, we set our y-coordinate equal to 0, which means we're going to be solving the equation 0 equals negative quantity x plus 2 squared plus 4. I'm going to add this square to both sides. We're going to have the x plus 2 squared equals 4. We'll then take square roots of both sides of the equation-- x plus 2 equals plus or minus the square root of 4, which is plus or minus 2. So we have x equals negative 2 plus or minus 2, which gives us two x-intercepts-- x is equal to negative 2 plus 2 and then x is equal to negative 2 minus 2. So in the first case, we come up with x equals 0, which we'd already seen. In the second case, that's a negative 2 minus 2. We have x equals negative 4, which indicates that this point on our graph is actually at the x-intercept at negative 4. So we have our two x-intercepts. We'd already identified our vertex-- our vertex is at negative 2 comma 4-- and we have the parabola opening downward. So let's think of some other properties that we can talk about with this particular function. We know that the domain is going to be the set of all real numbers. We can see that either by looking at the graph and noticing that if we scan it from left to right, we pick up all values of x. We can also see that we're just adding 2 to a value of x. We can do that to any number. We can square any number we'd like, we can take the negative of any number, and we can add 4 to any number. So there's no restrictions on what we can do to the value of x, so our domain is the set of all real numbers. Using the graph, we can see that our range is going to be values that are from negative infinity all the way up to the vertex, which has a y-coordinate of 4. So our range would be from negative infinity to 4, including the value of 4. We've identified the vertex by using our transformations, and our vertex has the coordinates negative 2 comma 4, and that leads us to our axis of symmetry. The axis of symmetry for a parabola must go through the vertex. And it's going to be a vertical line, because we can see that this vertical line is going to split that parabola in half, so its equation is going to be x equals, and the x value has to be the same as the x value of the vertex. So x equals negative 2 is going to give us our axis of symmetry. So altogether, using what you'd learned previously about transformations is going to help you see what's going on in general with a parabola of this format. So now we're going to generalize that. So let's summarize what we just saw. The vertex form of the equation of a quadratic function is f of x equals a times x minus h quantity squared plus k. That is, if we can put our function into this format, we can read off the vertex of the parabola, because you're going to see that you have a shift that's horizontal of h units and a shift vertical of k units. So the point that was originally at the origin has now moved to the point h comma k. So our vertex has those coordinates-- the points h comma k. The axis of symmetry is going to be the vertical line that's going to go directly through the vertex, so its equation is going to be x equals our h value. If our a value is positive, the parabola will open upward and the y-coordinate of the vertex is going to be a minimum value of f of x. So think about it this way-- you open upward, that point is going to be at the very bottom. If you look at the y-coordinate, it's going to be the lowest value for y that you can have. Alternatively, if our a value is negative, the parabola will open downward because of the reflection and the y-coordinate of the vertex is going to be a maximum value of f of x, because now it's going to be the highest value of y that you're able to get. So as long as we have a function given to us in vertex form, it's easy to graph the parabola. But now we're going to look at an example where we're not giving it in vertex form and we want to see how to proceed from that vantage point. The function I'm going to look at is f of x equals x squared minus 6x minus 7. So there's a couple of techniques we can use in order to accomplish this. I'm going to show you one with this example. That is, I'm going to begin by trying to find the x-intercepts. So recall that we can find x-intercepts by allowing the y value to equal 0 since we're not going to be moving up or down. So I'm going to take the function, replace f of x with 0, and solve the equation. That will give us 0 equals x squared minus 6x minus 7. Now, this quadratic is factorable. Let's proceed by writing down the factors. And we can take x squared, factor it as x times x, take 7, factor it as 7 times 1. Then when we look at our inner term, we have 7x. Our outer term is 1x. To combine those and end up with a negative 6x, we need to put a minus sign in front of the and a plus sign in front of the 1. We now need to double check that when we look at our last terms in this product that we end up with a negative 7, which we do. Now using the zero product property, we can set each factor equal to 0. So that gives us x minus 7 equals 0 or x plus 1 equals 0, leading us to x equals 7 and x equals negative 1. Now we have the symmetry that that's part of a parabola, and I'm going to use that idea in order to find the vertex, in that from the vertex on the x value, you have to go the same amount to the left and to the right in order to end up with any intercepts for the x-intercepts. So I'm going to look at finding the x-coordinate of the vertex by taking the average of my two x-intercepts. Again, when we look at the graph, it will make a little bit of sense. We're going to have our x-coordinate of the vertex. It's going to be midway between the two x-intercepts. So again, we can average the two x-intercepts, and the way to take an average is we add together. So I'm going to take 7 plus negative 1 and divide by 2. So that's going to give us 6 divided by 2, which equals 3, which means that I have an x-coordinate of my vertex as the value 3. If we know what the x-coordinate is, then what is the y-coordinate? We can find that by simply evaluating f of 3. So back to my equation here, we're going to have 3 squared minus 6 times 3 minus 7. That's going to give us 9 minus minus 7, which is going to be negative 9 minus 7, which is equal to negative 16. So the y-coordinate of the vertex is going to be negative 16. Now let's put this together and look at the graph, and then see what we can say about a generalization of that process. So I'm going to quickly just sketch in a graph here, and what I want to do is-- let's make this an x, make this a y-- I'm going to place my x-intercepts. And notice that I have to have a y-coordinate down at negative 16, so let's think about the units we're going to use. I'm going to go ahead and go by units of 5. So this is going to be a 5, this is going to be a 10. Over here we'll have negative 5, negative 10. And then on my y-axis, let's use the same units, so 5, 10, and we need to go negative 5, negative 10, negative 15, and negative 20 in order to end up getting down to this negative 16 which I need for my y-coordinate. Again, I'm going to place the x-intercepts on the graph. So here I have an x-intercept at 7-- let's just make a big dot. I have an x-intercept at negative 1-- that's going to be approximately right here. And once more, just reviewing the process that we used, because of the symmetry of the parabola, I know that my vertex needs to be midway between these two x-intercepts. And we determined that that x-coordinate would be x equals 3. So again, midway between 7 and negative 1 is the value of 3. I'm just going to mark a 3 right here just so you can see what I'm looking at. Here's 7, here's negative 1, and I want to go down to negative 16, so that's approximately right here. And see how my vertex will line up between the two if we look at it on a horizontal type of field? I can now look at my y-intercept, because that's always a good point to find. We can find the y-intercept by looking at the original function and substituting in a value of for x. So again, y-intercept is going to equal f of 0. Substituting gives us 0 squared minus 6 times 0, which is 0, minus 7. So what I end up with is f of 0 equals negative 7. Let's plot that point on our axis about right there. And now, really, all we're going to do is connect the dots in order to come up with our parabola. So we want to come down here, end up going through the y-intercept, round it off as a kind of a U shape, come back up through the 7, and then continue on upward. So notice I'm able to draw in this parabola with really only plotting one, two, three, four points. The important point to find is the vertex, because I know that that's where the symmetry is going to be guaranteed on the right and the left side. In fact, we want to recognize we have an axis of symmetry-- that's going to be the vertical line that is going to go through the vertex. So I'm going to end up with an axis of symmetry at x equals the x-coordinate of the vertex, which is 3. We can also note that we can look at our graph and determine some other graphing attributes. So let's just list some of those. For instance, what is the domain of the function? We can think of scanning the function from left to right, and notice that we're going to pick up all x values. We could also look at the equation of the function and say we can square any number, we can multiply any number times negative 6, we can subtract 7 from any number. In other words, there are no restrictions when I look at the algebraic format here. So my domain will be the set of all reals, which will be from negative infinity to infinity, for our range. We want to look at the graph and notice that this is a parabola that opens upward, and of course, we could have seen that also from the leading coefficient, which is going to be the value 1. That range is going to go from the y-coordinate that is the smallest, which in this case is negative 16, all the way to positive infinity, including the negative 16. So we'll have negative 16 to infinity. Now, there are a couple of other things that we can point out. Because we now know the vertex of this function, we can write this function instead of in its general format-- x squared minus 6x minus 7-- in its vertex form. That is, we could rewrite f of x equals, and let's recall the vertex form. That's a times x minus h quantity squared plus k, where my h and my k are the coordinates of the vertex. What is this a value? Well, it's going to be the same a value back in the general format. So here, remember the general format is ax squared plus bx plus c. The a value is still going to equal the value of 1. So back over here, f of x can be written as 1 times x minus the x-coordinate of the vertex, which we determined was 3, plus the y-coordinate of the vertex, which we determined was negative 16, so that's plus negative 16. Let's just simplify that. We end up with f of x equals x minus 3 quantity squared minus 16. And this is going to be the vertex form of that parabola, or of that quadratic function, is another way to say it. So there are other attributes we can talk about once we get a graph drawn. For instance, we could talk about where the graph is increasing and where the graph is decreasing. So once you get a picture of your quadratic function, there are a lot of other things that you can answer by using the graph. And in particular, let's look at where this function is increasing and decreasing, and I'm just going to write those answers here-- increasing and decreasing. So recall that we always read a graph from left to right. So as I'm looking at this graph and I'm thinking about tracing it with my pen, I'm moving downward until I end up at the vertex. Now, when we're giving the answers in terms of increasing and decreasing, we always want to think of it in terms of x as we're moving from left to right. So for this first section, which would be from the left negative infinity all the way until you end up at the vertex-- and remember that the x-coordinate of this vertex is going to be 3-- so from negative infinity until I get to 3, what's occurring? Well, I'm moving downward, which means that the function is decreasing in that realm. So we're going to have this decreasing from negative infinity until I get to 3, and I'm going to not include 3 in that answer, and I'll talk about that in a moment. And then what happens once I get to the vertex? As I continue moving to the right, the graph is increasing the entire time, so from 3 to positive infinity-- and it's not because I'm going up, it's because I'm going right-- from 3 to positive infinity, it's going to be increasing. Now, I mentioned that I was going to discuss why I didn't include 3. It was basically because I don't want to include it as increasing and decreasing at the same point. This is actually where it changes from one to the other. So again, we graph the entire function. We can put it into its vertex form by finding the coordinates of the vertex. One of the methods for finding the coordinates of the vertex will be to take the average of the two x-intercepts if we have x-intercepts. So let's kind of summarize that in our next clip. So again, let's generalize what we discovered in our last problem. Now, you'll recall in the last problem that we had the x-intercept as our guide to finding the vertex. But also in that problem, we were able to factor. Well, what's another way to find x-intercepts when you're dealing with a quadratic function? And that's going to be using the quadratic formula in case it doesn't factor-- or even if it does, you could always go that route. So just reviewing, if we look at ax squared plus bx plus c equals 0, recall that the quadratic formula can give you the values for x when we're going to have it set equal to 0, which means they're going to be the x-intercepts. Our x will equal negative b plus or minus b squared minus 4ac divided by 2a. And of course, you should have this memorized by now. So I'm going to just do a little bit of manipulation here in order to find what we can think of as a formula for the vertex of a parabola. First of all, notice that because we have two terms in the numerator divided by a single term in the denominator, we can separate that into two terms. We have negative b over 2a plus or minus that radical square root of b squared minus 4ac divided by 2a. Well, remember we talked about moving to the same way from the right and the left in line with the axis of symmetry? So what we're really doing here is we're taking the negative b over 2a and we're adding and subtracting some constant value which, of course, is given by this other expression. But the key here is to understand that what we're looking at is taking the negative b over 2a, which would be right in the middle, and then moving the same amount to the right and the left. So this mimics what we did in the last problem. Well, what that means is, what is going to be the value of our vertex? It's going to be this negative b over 2a for our x-coordinate. So we can find the y-coordinate, of course, by substituting back in. So thinking about the problem that we just finished with, we found our x-intercepts. We then found the vertex by using the fact that using the x-intercepts, we have to go the same amount to the right and to the left in order to end up in the middle, which was going to be the vertex value. Using the quadratic function, we can see the same idea. If we start at negative b over 2a and we move right or left a constant value, we would end up with our x-intercepts. So therefore, the x-coordinate of the vertex must be given by the negative b over 2a. And then again, to find the y-coordinate, we would substitute back in to the function in order to find that value with the x-coordinate of the vertex. So now we're going to look at an example where we're going to use what we just found out. Find the vertex of the parabola whose equation is given by f of x equals 1/2 x squared minus 5x plus 1/2. So the thing about what we just determined is we were thinking about x-intercepts, but it turns out that even if we don't have any x-intercepts, we can still use the same formula. And that is that recall to find the vertex, we can use the formula negative b divided by 2a, and then we'll evaluate that back in the function in order to find the y-coordinate of the vertex. So let's start off by identifying the values for our a and our b. Our a value is going to equal the coefficient of the x squared. So in our function, we notice that the coefficient of x squared is 1/2. Our b value is out coefficient of x. So in our case, the b value is equal to negative 5. So now we're just simply going to use the formula in order to find the vertex. We can think of the vertex as being h, which we've used that variable before. So our h is going to equal the negative b divided by 2a. So negative b means I'm going to take the opposite sign of b. That's going to give us 5. We're going to divide that by twice the a value, so that's going to be 2 multiplied times 1/2. Let's just simplify-- we're going to have 5 divided by 2 times 1/2, which is 1. And so we come up with our h value equal to 5. That means this is the x-coordinate of the vertex. To find the y-coordinate of the vertex, we're going to label it as k-- remember, hk is the vertex. We're going to have our k value given by f of 5. So that means I'm going to go back to my functional definition and I'm going to substitute in the value of 5. That will be 1/2 multiplied times 5 squared minus 5 times 5 plus 1/2. So this is going to give us 1/2 times 25 minus 25 plus 1/2. Let's go ahead and multiply here-- 1/2 times 25 is going to be 25 divided by 2, and then we have the minus 25 plus 1/2. Now notice that my first and my third term here both are in halves, so I can add 25 halves plus 1/2. That's going to give us 26 halves, then minus 25. 26 halves-- we can go ahead and divide. That's going to be 13. 13 minus 25 is going to equal negative 12. So we've found the x-coordinate of the vertex. That's going to give us the value of 5-- so our vertex is going to be 5 comma-- and we found the y-coordinate of the vertex-- that's going to be negative 12. And so we've been able to answer the question "Find the vertex of this parabola." Its coordinates are 5 comma negative 12. We're going to proceed with another example where we're going to be looking for finding the vertex of a parabola, but in this example I want to demonstrate another method for doing that. You recall that we have two methods so far. One is to find the x-intercepts of the function and then take the average of the two x-intercepts to find the x-coordinate of the vertex, and once we have the x-coordinate, we can find the y-coordinate by substituting in. The second version is to try to find the x-coordinate of the vertex by using the idea of taking that negative b over 2a from the quadratic formula, using that formula process, and then again finding our y-coordinate. You may recall, however, that the quadratic formula was derived by completing the square on the format of ax squared plus bx plus c equals 0. Let's say you're proficient at completing the square. Well, that gives us now a third method for finding the vertex of the parabola. Here's our question, or our problem, we should say-- we want to find the vertex of the parabola whose equation is given by f of x equals 3x squared minus 12x plus 5. And what I'm going to do is take the expression that's to the right and then going to complete the square and put it into the vertex form of a parabola that we've seen previously. So let's go ahead and do that. And the only thing about it is that when you completed the square before, you were working with an equation where you were working on both sides of the equation. In this process, we're going to only work on the same side of the equation. That is, I want to always just have f of x equals and not put anything on the left-hand side. So recalling the process for completing the square, you may remember that we isolate our x terms-- that is, terms that have the variable x in them-- and we end up with a leading coefficient of 1. So to do that, I'm going to do it in two steps. I'm going to think about it as 3x squared minus 12x, just separating that from the plus 5 here. And then in my next step, I'm going to go ahead and factor out the 3 only from the terms that involve the variable x. So this is going to have a 3, and then I'm going to have my x squared minus 4x. And now I'm going to leave some room here because I know I want to complete the square, and then I have this plus 5 to follow up. To review the process for completing the square, recall that we take half of the middle coefficient-- that would be half of this negative 4, so let's just write it over to the side. It's 1/2 of negative 4, which is going to equal negative 2. We then take that value, negative 2, and we square it. That's equal to the value of 4. This is going to be the value that I'm going to add inside of the parentheses. So just to kind of color code it, I'm going to put plus 4. Now, notice that I've got a addition of 4, but that's inside parentheses. I've got to always compensate for something that I've added to the expression. That 4 is being multiplied times 3, so what I have in effect put on this side of the equation is an addition of 12. To compensate for an addition of 12, we need to subtract 12 off so that this expression is still equivalent to the step that we had previously. You should probably take some time to multiply it out just to see for yourself. You have the 3x squared here minus 12x-- that's what we had before. This 3 times 4 gives me 12. So I've got an extra 12, and then the plus 5 moves down and the minus 12 compensates so that what we have is still equivalent to our previous step. But now what we have in parentheses is a perfect square. So we can rewrite this expression as 3 times the quantity x minus 2 squared. And I'll go ahead and combine 5 minus to give me the negative 7. So rewriting this, we have 3 times x minus 2 quantity squared minus 7-- that's the vertex form for this parabola. We can now read off the vertex by using x minus h-- that's going to be my h value and my k value, and the h value's going to equal 2, and the k value is this constant at the end, which is negative 7. So my vertex is going to have the coordinates comma negative 7. Again, just to review the process, we want to complete the square on the expression that we have, making sure that whatever we do add to the equation is compensated for on the far end. If you're multiplying by a number here, you have to make sure that you multiply through in order to decide what to subtract off or, if this had happened to be a negative, what you would add back in. So just make sure that you're compensating for what you've added to the expression. Then once you write it into its vertex form, you can read off the vertex of the parabola. It's time for a quick quiz. What is the vertex of the parabola y equals negative x squared minus 6x plus 5? Is the correct answer A. The ordered pair negative 3, 14. B. The ordered pair negative 3, 32. C. The ordered pair 3, negative 22. D. The ordered pair 3, 5. Choose A, B, C or D now. You're correct, the answer is A. The vertex of the parabola is the ordered pair negative 3, 14. Sorry the correct answer is A, the ordered pair negative 3, 14 is the vertex of the parabola. To find the vertex of this parabola one way we can do it is to use the format where we're going to have the h value of the vertex equal to negative b divided by 2a. So I can solve for that value of h which is going to be the x coordinate is going to equal the negative of negative 6 which is my coefficient of x that's the B value divided by 2 times the coefficient of x squared which the A value and that's a negative 1. Simplifying I end up with h equals negative this would be negative 6 divided by a negative 2. So that's going to equal a positive 3 and when I take the negativity up, negative of it we end up with negative 3. So the x coordinate of a vertex is going to be negative which eliminates C and D from this process. Now we need to find the y coordinate the vertex. We can find that y coordinate which I'm going to call k by substituting the value of x into our function which is given as y equals will have a negative of negative 3, quantity squared minus 6 times negative 3 plus 5. So the key thing here is to remember that you're going to square the negative value first before you take the negative of that value. So our k is going to equal the negative of, negative 3 squared which is 9, so that's going to be negative 9. We have negative 6 multiplied times negative 3 sets plus and then we end up with plus 5. So simplifying further our k values is going equal negative 9 plus 18 which is positive and 9 plus 5 is going to be 14. Giving us an x coordinate of negative 3 and a y coordinate of for the vertex of this parabola. Now, when we think about linear functions, we know that if we have two points, that determines a line. When we look at quadratic functions, it turns out that we would have to have three points to determine a quadratic function in general. However, it turns out if that one of those points is actually the vertex, then we don't have to have all three points. We're going to use this in our next example. Determine the quadratic function whose vertex is negative 2 comma 3 and whose y-intercept is 11. So notice that I'm really only given two points, but one of those points is the vertex, and that's going to allow us to use the vertex form for the parabola that we are accustomed to. In other words, recall that if we have f of x equals a times x minus h squared plus k, this is the vertex form for a quadratic function. What we're told in the problem is that our vertex is negative 2 comma 3, and what that means is that our h value is equal to negative and our k value is equal to 3. Now, what we're not told in the problem is our a value, and of course, we're also given some extra information that I'm going to use in a moment. But at this point, notice that I can substitute in to my vertex form and say OK, great, f of x must equal some value of a, which I'm going to have to determine in a moment. And then I'm going to have in parentheses x minus a negative 2, which is going to be the same as x plus 2 squared, and then the k value is 3, so we can just put plus 3. Now, what I now need to use is the extra bit of information that I had in the problem. We are told that the y-intercept is equal to 11, and so if our y-intercept is equal to 11, what is the point on the graph that corresponds to that? Well, a y-intercept means it hits along the y-axis, which means that you aren't moving to the right or the left, and therefore the x-coordinate is going to be 0. So our point is 0 comma 11. We'll notice that this gives us an x and a y value, and that has to fit with the definition of the function. All points on this parabola have to fit that equation and make it true. So I can substitute in the value of 11 for f of x, and I'll do that over here-- that's my y value. It's equal to my a value that I don't know yet multiplied times the x value of 0. And then let's write the rest of the equation, so plus 2 quantity squared plus 3. So one more time, just reviewing the concept. You've been able to come up with the vertex form of that function. We don't know the value of a, but we're able to substitute for x and for y, giving us an equation that only has a single variable in it. That means we can now solve for a. So 11 is going to equal a multiplied times squared, which is going to be times 4 plus 3. Let's subtract 3 from both sides of the equation. We end up with 8 equals a times 4 and now dividing by 4, we end up with 2 equals a. So going back to the vertex form of the function, we can have f of x equals. Now we're able to substitute for a, so we're going to have our 2, times x plus 2 quantity squared plus 3. This is going to be the functional format for this parabola. It's time for another quick quiz. By finding the vertex of a parabola and knowing which direction it opens, one can determine how many x-intercepts will be on its graph. Use this process to decide how many x-intercepts are on the graph of y equals negative 2 times the quantity x plus one squared minus 3. Is the answer A. 0 x-intercepts. B. 1 x-intercept. or C. 2 x-intercepts. Choose from A, B and C now. You're correct, the answer is A, there are 0 x-intercepts on this graph. Sorry the answer is A, there are 0 x-intercepts for this graph. To understand the answer we have to first find the vertex of the parabola. Now this is written in vertex form. In that we can read off the vertex by using the fact that this is a shift to the left of one unit and then down 3. So our vertex is going to have coordinates negative 1 comma negative 3. In the vertex format we note that the value of a is a negative value which means that this parabola is going to open downward. Let's just do a really quick sketch. What I can think about is that if I think about the x y plane and I plot the vertex at the point negative 1 negative 3. And this parabola opens downward. Then there's no way I'm going to have any x-intercepts. So putting this all together gives us our correct result of A, with 0 x-intercepts. Now, one of the applications that's common to see when you're working with quadratic functions is going to be called an optimization problem. When you try to optimize something, you want to make it as efficient or the best it can possibly be, in general. In mathematics, when we're looking at optimizing something, typically we're looking at finding either a maximal or a minimal value for an expression. So here's the problem that we want to consider. We have a word problem that says the height in meters of a projectile, shot straight up in the air at an initial velocity of 22 meters per second from an initial height of 2 meters, can be found using the function h of t equals negative 4.9 times t squared plus 22t plus 2, where t is the number of seconds after it has been shot. The question is, what is the maximum height the projectile will reach? So again, this is our optimization that we're looking for. Now, whenever you're given a word problem, one thing you want to make sure you do is understand what the variables are representing in the expression that we're given. So notice that we have two variables in this problem. We have an h and a t. We have h of t as a function-- that's basically f of x. Our t value is our x-coordinate in this expression. So t stands for the number of seconds after this projectile's been shot. The h in the problem stands for the height of the projectile in meters, so we can determine how high the projectile has gone over time. Now, if we're trying to find the maximum height, think about the format of this function. It's quadratic-- it has the format ax squared plus bx plus c. The a value is negative, and remember that that tells you that we have a parabola that opens downward. So the vertex of that parabola is going to be giving us the maximum height as the y-coordinate of the vertex. Now, to determine how to proceed, you really want to think about all the different methods that we have. We've seen so far that we could find x-intercepts and then take an average in order to define the x-coordinate of the vertex, but that doesn't really seem to be the maximal way to do this one. We could complete the square, but again, the numbers that are involved are fairly involved, so let's not use that. Instead, remember that we have a formula format that we could use. We can find the vertex of a parabola by using the x-coordinate as negative b over 2a and the y-coordinate is then going to be found by substituting the x-coordinate into our function. What we're interested in in this problem is going to be finding the maximum height, which means we're going to be looking for the y-coordinate of the vertex. But first, we have to find the x-coordinate. So we're going to find that value by saying that our t value, which is like x, is equal to negative b divided by 2a. Let's determine what the value of b is going to equal. That's going to be the value of 22, because the b value is always going to be the coefficient of our middle term or our linear part. So we're going to have the 22 multiplied times t to the first power-- that means that b is equal to 22. So we're going to have negative 22 divided by multiplied times our a value. Our a value is going to be the coefficient of our squared term-- in this case, it's t squared. So our a value is going to be the negative 4.9. Now, we can use a calculator in order to come up with an approximation for this, and I've done this previously. We have that t in this case is approximately equal to 2.245, and since it's a work problem, let's go ahead and put the unit on it-- that's in seconds. So 2.245 seconds after the projectile has been launched, it's going to reach its maximal height. To find that maximal height, we're going to substitute in to the function. Now, I have f of whatever, because this is the format that we had, but remember in our case, we're looking at h of t. So I'm going to find the y-coordinate of the vertex by finding h of 2.245. That's going to be the height at 2.245 seconds. And once more, just-- we're going to take that and substitute it into our function, which would require us to do this. We're going to have the negative 4.9 multiplied times 2.245 quantity squared plus we'd have to have 22 multiplied times 2.245, and then we'd have that added to the value of 2. So taking out a calculator and substituting in the expression that we see here, we come up with our h value approximately equal to 26.7. And recall that our h value is given in meters, so we're going to have 26.7 meters as the maximum height that the projectile will end up reaching. Once more, just kind of to reiterate, we have a quadratic function. It's going to be a parabola that opens downward. We can find the maximum value by looking for the vertex, and I've used the format where I have a formula that we can work with in order to do so. So in conclusion, we've looked at a number of different methods for finding the vertex of a parabola. And we've also looked at some of the properties of a function that ends up being parabolic or quadratic. So you need to review this on your own. And the thing is that when you're working with these problems, you have to have some familiarity in order to determine what the best process is going to be, dependent on the numbers that are involved, the expressions that we're working with, what's given to you. You know, it's a typical type of a process, where you want to become more familiar with what you're dealing with in order to determine the best method to proceed with. So it's time for you to try some more problems on your own to gain that familiarity. Good luck.
Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
4. Polynomial Functions
Quadratic Functions
Video duration:
6mPlay a video:
Related Videos
Related Practice