Graph each piecewise-defined function. See Example 2. ƒ(x)={6-x i...

Question

Graph each piecewise-defined function. See Example 2. ƒ(x)={6-x if x≤3, 3 if x>3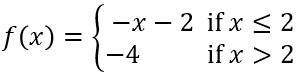

Piecewise function f(x) with two conditions: -x-2 for x≤2 and -4 for x>2.

Accepted Answer

Hey, everyone here we are asked to graph the following function F of X is equal to negative X minus two. If X is less than or equal to two and negative four. If X is greater than two, here we have four answer choice options. ABC and D, each of which display a graph representing our given function. So to graph our given function, we just need to graph each interval of the domain separately. So we can begin by considering the first interval of our function where we have f of X is equal to negative X -2, which is defined for when X is less than or equal to two. So the first step here is to just substitute in values for X into our function. So we can obtain ordered pairs. So we can begin with the highest value of X according to the inequality. So we can begin with having X be equal to two. So we need to substitute N 24, X in our function. So we have F of two is equal to negative two minus two. Simplifying we get negative four. And so we see the first ordered pair that we have is two and negative four. So now we just want to repeat this procedure for other values of X that are now less than two. So we can obtain more ordered pairs. So we can choose the value, let's say have X be equal to zero. So we have F of zero, which gives us zero minus two. Simplifying we get negative two. So we see a second ordered pair is zero and negative two. Now repeating this process one more, we can have X B equal to one. So we have F of one is equal to negative one minus two. Simplifying we get negative three. So we see a third ordered pair is one and negative three. So now with these three ordered pairs, the next step is to plot these points on a graph. So plotting these points, we see we have our three individual points plotted on a single graph. And so we have begun graphing the first interval of our function. So the next step is to draw a line that connects these points so that we have graphed our first part of the function. And in doing this, we see we have an end point of the line at two and negative four. And we see that this is a solid endpoint set. We know that our function f of X is equal to negative X -2 is defined for when X is equal to two. So again, we get a solid end point. And then we see the line extends all the way to negative infinity since X can also be less than two. So now we have graphed the first part of our given function. So now it is time to consider the second interval of our function where we have F of X is equal to negative four, which is defined for when X is greater than two. So now with this second interval, we see that we will have a horizontal line since F of X is equal to negative four is defined as Y is equal to negative four. So we will have a horizontal line at Y is equal to negative four and it will extend from X is equal to two all the way till positive infinity since X is going to be greater than two. And so graphing this line here graphing this second part of our original function, we see again, we have this horizontal line in orange where Y is equal to negative four. And we see that we go from X is equal to two all the way till positive infinity. But we also can notice that for this function F of X is equal to negative four. It is undefined for when X is equal to two. So if this line was graphed alone, it would have a hollow circle as the end point. But here we have both of our lines graph and they are joined at X is equal to two. And so with this final graph, we are left with answer choice B thanks for watching. I hope you found this video helpful and I'll see you again next time.

Graph each piecewise-defined function. See Example 2. ƒ(x)={6-x if x≤3, 3 if x>3

Key Concepts

Piecewise Functions

Graphing Techniques

Continuity and Discontinuity

Watch next