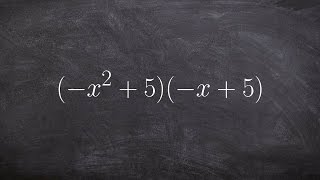Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
Multiplying Polynomials
Problem 23a
Textbook Question
Textbook QuestionIn Exercises 23–34, find each product using either a horizontal or a vertical format. (x−3)(x²+2x+5)
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
7mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Polynomial Multiplication
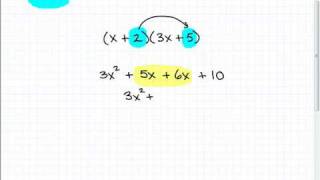
Polynomial multiplication involves distributing each term of one polynomial to every term of another polynomial. This process can be done using the distributive property, ensuring that all combinations of terms are multiplied together. For example, in the expression (x−3)(x²+2x+5), each term in the first polynomial must be multiplied by each term in the second polynomial.
Recommended video:

Finding Zeros & Their Multiplicity
Horizontal and Vertical Formats
Horizontal and vertical formats refer to different methods of organizing polynomial multiplication. The horizontal format lays out the polynomials side by side, while the vertical format stacks them, similar to traditional arithmetic multiplication. Choosing between these formats often depends on personal preference or the complexity of the polynomials involved.
Recommended video:

Horizontal Parabolas
Combining Like Terms
Combining like terms is a crucial step in simplifying the result of polynomial multiplication. After distributing and multiplying all terms, any terms that have the same variable raised to the same power can be added or subtracted. This process helps to condense the polynomial into its simplest form, making it easier to interpret and use in further calculations.
Recommended video:

Combinations
Related Videos
Related Practice