Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
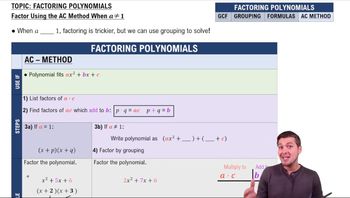
Factoring Polynomials
Problem 72b
Textbook Question
Simplify each complex fraction. (2 - 2/y) / (2 + 2/y)
 Verified step by step guidance
Verified step by step guidance1
Identify the complex fraction: \( \frac{2 - \frac{2}{y}}{2 + \frac{2}{y}} \).
Find a common denominator for the terms in the numerator and the denominator. Here, the common denominator is \( y \).
Rewrite the numerator: \( 2 - \frac{2}{y} = \frac{2y}{y} - \frac{2}{y} = \frac{2y - 2}{y} \).
Rewrite the denominator: \( 2 + \frac{2}{y} = \frac{2y}{y} + \frac{2}{y} = \frac{2y + 2}{y} \).
Simplify the complex fraction by dividing the rewritten numerator by the rewritten denominator: \( \frac{\frac{2y - 2}{y}}{\frac{2y + 2}{y}} = \frac{2y - 2}{2y + 2} \).
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Complex Fractions
A complex fraction is a fraction where the numerator, the denominator, or both contain fractions themselves. To simplify complex fractions, one typically eliminates the inner fractions by finding a common denominator or multiplying through by the least common multiple (LCM) of the denominators involved.
Recommended video:

Complex Conjugates
Finding a Common Denominator
Finding a common denominator is essential when adding, subtracting, or simplifying fractions. In the context of complex fractions, it involves determining a common base for the denominators of the inner fractions, allowing for easier manipulation and simplification of the overall expression.
Recommended video:
Guided course

Rationalizing Denominators
Simplifying Rational Expressions
Simplifying rational expressions involves reducing fractions to their simplest form by canceling common factors in the numerator and denominator. This process is crucial in complex fractions, as it helps to clarify the expression and make calculations more manageable.
Recommended video:
Guided course

Simplifying Algebraic Expressions

 7:30m
7:30mWatch next
Master Introduction to Factoring Polynomials with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice