Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
2. Graphs of Equations
Graphs and Coordinates
Problem 13b
Textbook Question
Determine the intervals of the domain over which each function is continuous. See Example 1. 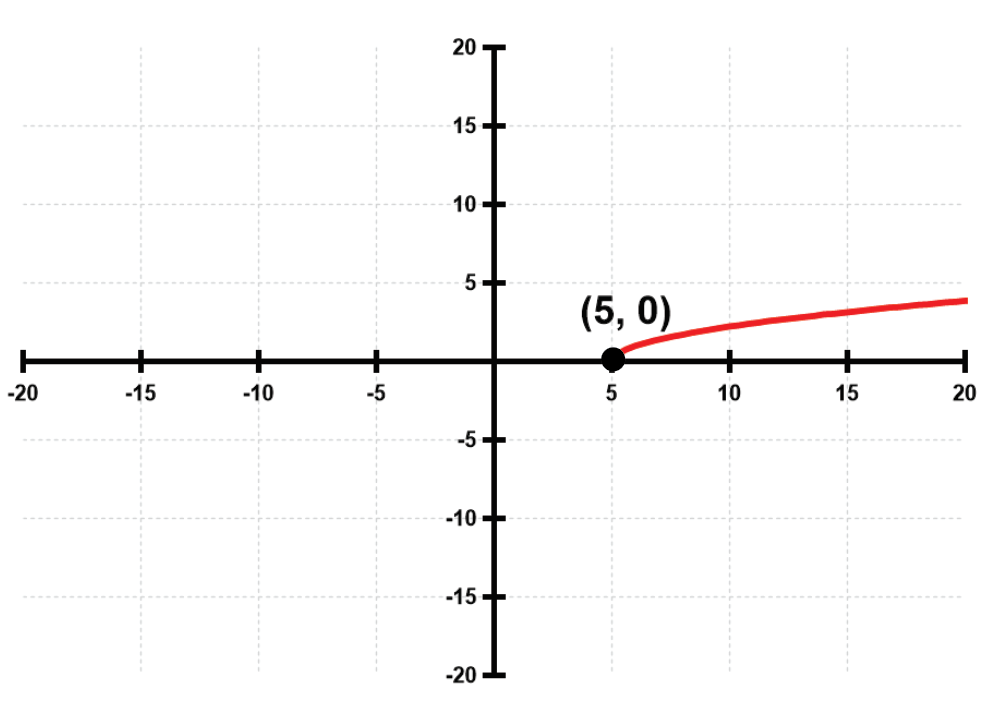
 Verified step by step guidance
Verified step by step guidance1
Identify the point of interest on the graph, which is (5, 0).
Observe the behavior of the function around this point. The function starts at (5, 0) and continues to the right.
Determine if there are any breaks, holes, or jumps in the graph. In this case, there are none.
Conclude that the function is continuous from x = 5 to positive infinity.
Express the interval of continuity in interval notation: [5, ∞).
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Continuity of Functions
A function is continuous at a point if the limit of the function as it approaches that point equals the function's value at that point. For a function to be continuous over an interval, it must be continuous at every point within that interval, meaning there are no breaks, jumps, or holes in the graph.
Recommended video:

Graphs of Common Functions
Intervals of Continuity
Intervals of continuity refer to the ranges of the independent variable (usually x) where a function remains continuous. These intervals can be expressed in interval notation, indicating where the function does not have any discontinuities, such as vertical asymptotes or removable discontinuities.
Recommended video:

Interval Notation
Identifying Discontinuities
Discontinuities can occur in various forms, including removable (holes), jump, and infinite discontinuities. To determine where a function is continuous, one must identify these points by analyzing the function's behavior, particularly at critical points like where the function is undefined or where it changes direction.
Recommended video:
Determining Removable Discontinuities (Holes)

 5:10m
5:10mWatch next
Master Graphs & the Rectangular Coordinate System with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice