Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
5. Rational Functions
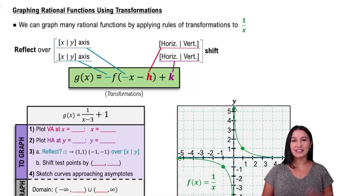
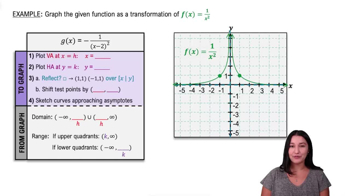
Graphing Rational Functions
Problem 9
Textbook Question
Textbook QuestionUse the graph of the rational function in the figure shown to complete each statement in Exercises 9–14. 
As x -> -3^-, f(x) -> __
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
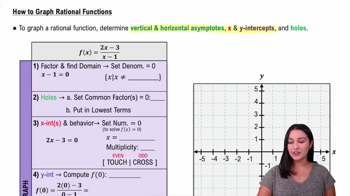
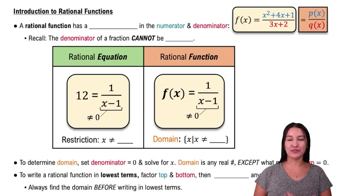
Rational Functions
A rational function is a function that can be expressed as the ratio of two polynomials. The general form is f(x) = P(x)/Q(x), where P and Q are polynomials. Understanding rational functions is crucial for analyzing their behavior, including identifying asymptotes and intercepts, which are key to interpreting their graphs.
Recommended video:
Intro to Rational Functions
Asymptotes
Asymptotes are lines that a graph approaches but never touches. Vertical asymptotes occur where the function is undefined, typically where the denominator equals zero, while horizontal asymptotes indicate the behavior of the function as x approaches infinity. In this case, the graph has vertical asymptotes at x=6 and x=14, and a horizontal asymptote at y=0.
Recommended video:

Introduction to Asymptotes
Limits
Limits describe the behavior of a function as the input approaches a certain value. In this context, evaluating the limit of f(x) as x approaches -3 from the left (denoted as x -> -3^-) helps determine the corresponding output value. Understanding limits is essential for analyzing the continuity and behavior of rational functions near their asymptotes.
Recommended video:

Interval Notation

 5:31m
5:31mWatch next
Master Graphing Rational Functions Using Transformations with a bite sized video explanation from Callie
Start learningRelated Videos
Related Practice