Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
7. Systems of Equations & Matrices
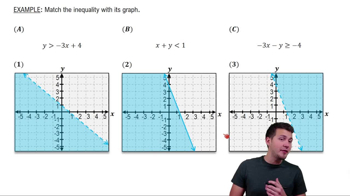
Graphing Systems of Inequalities
Problem 19a
Textbook Question
Textbook QuestionGraph each inequality. x ≤ 3
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Inequalities
Inequalities are mathematical expressions that show the relationship between two values when they are not equal. They use symbols such as ≤ (less than or equal to), ≥ (greater than or equal to), < (less than), and > (greater than). Understanding how to interpret and manipulate inequalities is essential for solving problems that involve ranges of values.
Recommended video:

Linear Inequalities
Graphing on a Number Line
Graphing inequalities on a number line involves representing the solution set visually. For the inequality x ≤ 3, you would draw a number line, place a closed circle on 3 to indicate that 3 is included in the solution, and shade to the left to show all values less than or equal to 3. This visual representation helps in understanding the range of solutions.
Recommended video:
Guided course

Graphing Lines in Slope-Intercept Form
Closed and Open Intervals
In the context of inequalities, closed intervals include the endpoints, while open intervals do not. For the inequality x ≤ 3, the closed interval notation is (-∞, 3], indicating that 3 is part of the solution set. Recognizing the difference between closed and open intervals is crucial for accurately representing solutions in graph form.
Recommended video:

Interval Notation

 7:2m
7:2mWatch next
Master Linear Inequalities with a bite sized video explanation from Patrick Ford
Start learning