Here are the essential concepts you must grasp in order to answer the question correctly.
Polynomial Long Division
Polynomial long division is a method used to divide a polynomial by another polynomial of lower degree. It involves dividing the leading term of the dividend by the leading term of the divisor, multiplying the entire divisor by this result, and subtracting it from the dividend. This process is repeated until the degree of the remainder is less than that of the divisor, resulting in a quotient and a remainder.
Recommended video:
Introduction to Polynomials
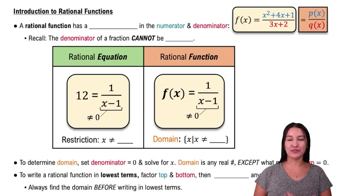
Rational Functions
A rational function is a function that can be expressed as the ratio of two polynomials. In the case of g(x) = (2x + 7)/(x + 3), the numerator and denominator are both polynomials. Understanding the behavior of rational functions, including their asymptotes and intercepts, is crucial for graphing them accurately.
Recommended video:
Intro to Rational Functions
Transformations of Functions
Transformations of functions involve shifting, stretching, compressing, or reflecting the graph of a function. For the function f(x) = 1/x, transformations can be applied to modify its graph, such as vertical shifts or horizontal shifts. These transformations help in visualizing how the graph of g(x) can be derived from f(x) by applying specific changes based on the quotient and remainder obtained from the long division.
Recommended video:
Domain & Range of Transformed Functions
 Verified Solution
Verified Solution


 6:4m
6:4m
