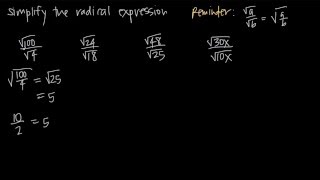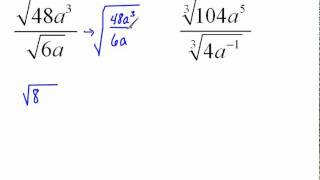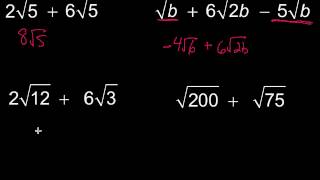Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
Radical Expressions
Problem 131
Textbook Question
Perform the indicated operations and/or simplify each expression. Assume all variables represent positive real numbers. ∜2/25
 Verified step by step guidance
Verified step by step guidance1
Identify the expression as a fourth root: \( \sqrt[4]{\frac{2}{25}} \).
Apply the property of radicals that allows you to separate the numerator and the denominator: \( \sqrt[4]{\frac{2}{25}} = \frac{\sqrt[4]{2}}{\sqrt[4]{25}} \).
Recognize that \( \sqrt[4]{25} \) can be simplified because 25 is a perfect square: \( \sqrt[4]{25} = \sqrt{5} \).
Substitute back into the expression: \( \frac{\sqrt[4]{2}}{\sqrt{5}} \).
Consider rationalizing the denominator if necessary, by multiplying the numerator and the denominator by \( \sqrt{5} \) to eliminate the radical in the denominator.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Radicals and Roots
Radicals involve the extraction of roots from numbers, such as square roots or fourth roots. The notation ∜ represents the fourth root, which is the value that, when raised to the fourth power, equals the original number. Understanding how to manipulate and simplify expressions involving radicals is essential for solving problems that require root calculations.
Recommended video:
Guided course

Expanding Radicals
Exponents
Exponents are a shorthand way to express repeated multiplication of a number by itself. For example, a number raised to the power of 1/4 indicates the fourth root of that number. Familiarity with the laws of exponents, including how to convert between radical and exponential forms, is crucial for simplifying expressions involving roots.
Recommended video:
Guided course

Rational Exponents
Simplification of Expressions
Simplifying expressions involves reducing them to their most basic form while maintaining equivalence. This process may include combining like terms, reducing fractions, and applying properties of exponents and radicals. Mastery of simplification techniques is vital for efficiently solving algebraic problems and ensuring clarity in mathematical communication.
Recommended video:
Guided course

Introduction to Algebraic Expressions
Related Videos
Related Practice