Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
7. Systems of Equations & Matrices
Introduction to Matrices
Problem 10c
Textbook Question
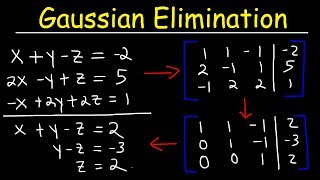
In Exercises 8–11, use Gaussian elimination to find the complete solution to each system, or show that none exists.
 Verified step by step guidance
Verified step by step guidance1
<Step 1: Write the system of equations in augmented matrix form.>
<Step 2: Use row operations to get a leading 1 in the first row, first column.>
<Step 3: Eliminate the entries below the leading 1 in the first column by using row operations.>
<Step 4: Move to the second row, second column, and repeat the process to get a leading 1 and eliminate entries below it.>
<Step 5: Continue this process for each column until the matrix is in row-echelon form, then back-substitute to find the solution.>
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
6mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Gaussian Elimination
Gaussian elimination is a method for solving systems of linear equations. It involves transforming the system's augmented matrix into row echelon form using a series of row operations, which include swapping rows, multiplying a row by a non-zero scalar, and adding or subtracting rows. This process simplifies the system, making it easier to find solutions or determine if no solution exists.
Recommended video:
Guided course

Solving Systems of Equations - Elimination
Row Echelon Form
Row echelon form is a specific arrangement of a matrix where all non-zero rows are above any rows of all zeros, and the leading coefficient of each non-zero row (the first non-zero number from the left) is to the right of the leading coefficient of the previous row. This structure is crucial for identifying the number of solutions in a system of equations, as it helps in back substitution to find the values of the variables.
Recommended video:
Guided course

Solving Systems of Equations - Matrices (Row-Echelon Form)
Consistency of a System
A system of linear equations is considered consistent if it has at least one solution, and inconsistent if it has no solutions. During Gaussian elimination, if a row reduces to a form that implies a contradiction (such as 0 = 1), the system is inconsistent. Understanding the consistency of a system is essential for determining whether to expect a unique solution, infinitely many solutions, or none at all.
Recommended video:
Guided course

Classifying Systems of Linear Equations

 4:35m
4:35mWatch next
Master Introduction to Matrices with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice