Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
7. Systems of Equations & Matrices
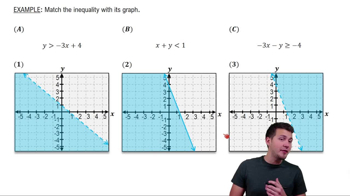
Graphing Systems of Inequalities
Problem 59a
Textbook Question
Graph the solution set of each system of inequalities.
2x+3y≤12
2x+3y>−63x+y<4
x≥0y≥0
 Verified step by step guidance
Verified step by step guidance1
Start by graphing the first inequality: \(2x + 3y \leq 12\). To do this, first find the boundary line by setting \(2x + 3y = 12\). Find the x-intercept by setting \(y = 0\), which gives \(x = 6\). Find the y-intercept by setting \(x = 0\), which gives \(y = 4\). Plot these intercepts and draw the line. Since the inequality is \(\leq\), shade the region below the line.
Next, graph the second inequality: \(2x + 3y > -6\). The boundary line is \(2x + 3y = -6\). Find the x-intercept by setting \(y = 0\), which gives \(x = -3\). Find the y-intercept by setting \(x = 0\), which gives \(y = -2\). Plot these intercepts and draw the line. Since the inequality is \(>\), shade the region above the line.
Now, graph the third inequality: \(3x + y < 4\). The boundary line is \(3x + y = 4\). Find the x-intercept by setting \(y = 0\), which gives \(x = \frac{4}{3}\). Find the y-intercept by setting \(x = 0\), which gives \(y = 4\). Plot these intercepts and draw the line. Since the inequality is \(<\), shade the region below the line.
Graph the fourth inequality: \(x \geq 0\). This represents the region to the right of the y-axis, including the y-axis itself.
Finally, graph the fifth inequality: \(y \geq 0\). This represents the region above the x-axis, including the x-axis itself. The solution set is the region where all shaded areas overlap, considering all inequalities.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
12mPlay a video:
Was this helpful?

 7:2m
7:2mWatch next
Master Linear Inequalities with a bite sized video explanation from Patrick Ford
Start learning