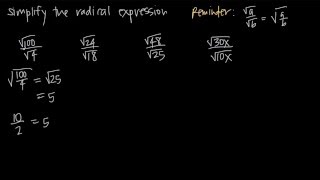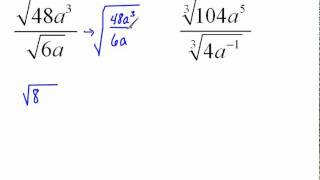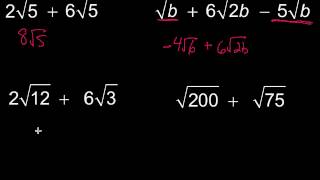In Exercises 85–116, simplify each exponential expression. x³/x⁹

Verified step by step guidance

1. Identify the base of the exponential expressions, which is \( x \) in both the numerator and the denominator.
2. Apply the quotient rule for exponents: \( \frac{a^m}{a^n} = a^{m-n} \).
3. Subtract the exponent in the denominator from the exponent in the numerator: \( x^{3-9} \).
4. Simplify the expression by performing the subtraction: \( x^{-6} \).
5. Recognize that a negative exponent indicates a reciprocal: \( x^{-6} = \frac{1}{x^6} \).

Key Concepts

Exponential Rules

Exponential rules are fundamental properties that govern the manipulation of expressions involving exponents. Key rules include the quotient rule, which states that when dividing two exponential expressions with the same base, you subtract the exponents: a^m / a^n = a^(m-n). Understanding these rules is essential for simplifying expressions like x³/x⁹.

Negative Exponents

Negative exponents arise when the base is in the denominator of a fraction. For example, x^(-n) is equivalent to 1/x^n. This concept is crucial when simplifying expressions, as it allows for the transformation of negative exponents into positive ones, facilitating easier calculations and clearer results.

Simplifying Fractions

Simplifying fractions involves reducing them to their simplest form by dividing the numerator and denominator by their greatest common factor. In the context of exponential expressions, this means applying the rules of exponents to combine and reduce terms effectively, leading to a clearer and more concise expression.