Here are the essential concepts you must grasp in order to answer the question correctly.
Linear Equations
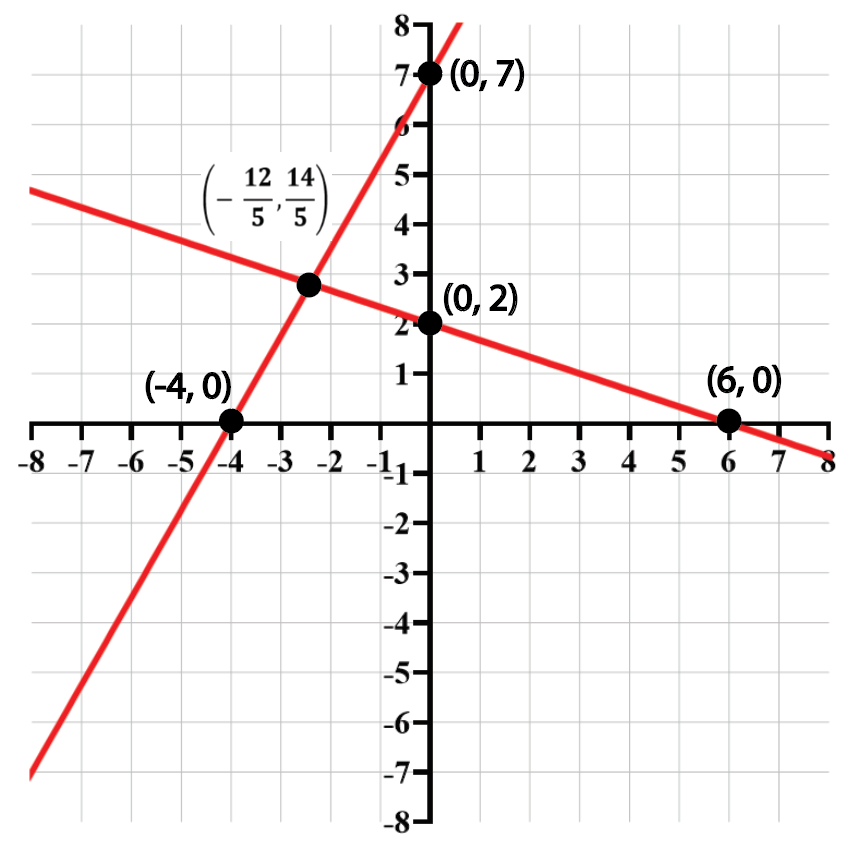
Linear equations are mathematical statements that describe a straight line when graphed on a coordinate plane. They can be expressed in various forms, including slope-intercept form (y = mx + b) and standard form (Ax + By = C). Understanding how to derive these equations from a graph is essential for solving problems involving linear relationships.
Recommended video:
Categorizing Linear Equations
Standard Form of a Linear Equation
The standard form of a linear equation is typically written as Ax + By = C, where A, B, and C are integers, and A should be non-negative. This form is useful for quickly identifying intercepts and is often required in problems involving systems of equations. Converting from slope-intercept or point-slope forms to standard form is a common task in algebra.
Recommended video:
Standard Form of Line Equations
Graphing Linear Equations
Graphing linear equations involves plotting points that satisfy the equation on a coordinate plane. Key points include the x-intercept (where the line crosses the x-axis) and the y-intercept (where it crosses the y-axis). Understanding how to identify these points from a graph is crucial for writing the corresponding equations and analyzing the relationships between variables.
Recommended video:
Categorizing Linear Equations