Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
7. Systems of Equations & Matrices
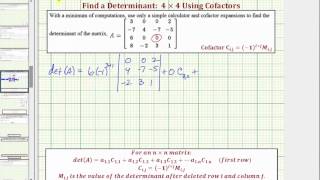
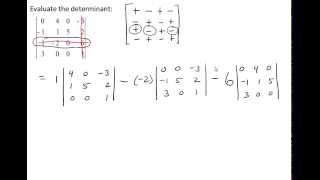
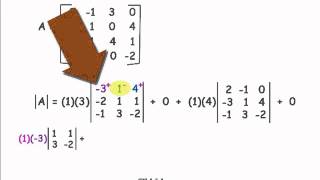
Determinants and Cramer's Rule
Problem 9c
Textbook Question
In Exercises 1 - 12, find the products AB and BA to determine whether B is the multiplicative inverse of A.
1 2 3 7/2 - 3 1/2
A = 1 3 4 B = - 1/2 0 1/2
1 4 3 - 1/2 1 - 1/2
 Verified step by step guidance
Verified step by step guidance1
Multiply matrix A by matrix B to find the product AB. Use the formula for matrix multiplication: (AB)_{ij} = \sum_{k=1}^{n} A_{ik}B_{kj}.
Calculate the first row of AB by multiplying the first row of A with each column of B and summing the products.
Calculate the second row of AB by multiplying the second row of A with each column of B and summing the products.
Calculate the third row of AB by multiplying the third row of A with each column of B and summing the products.
Multiply matrix B by matrix A to find the product BA. Use the same matrix multiplication formula and check if both AB and BA result in the identity matrix.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
15mPlay a video:
Was this helpful?

 4:36m
4:36mWatch next
Master Determinants of 2×2 Matrices with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice