Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
1. Equations & Inequalities
Linear Inequalities
Problem 10
Textbook Question
Use the graph to solve each equation or inequality. Use interval notation where appropriate. 2(X-2) / {(X-1)(X-3)} ≤ 0 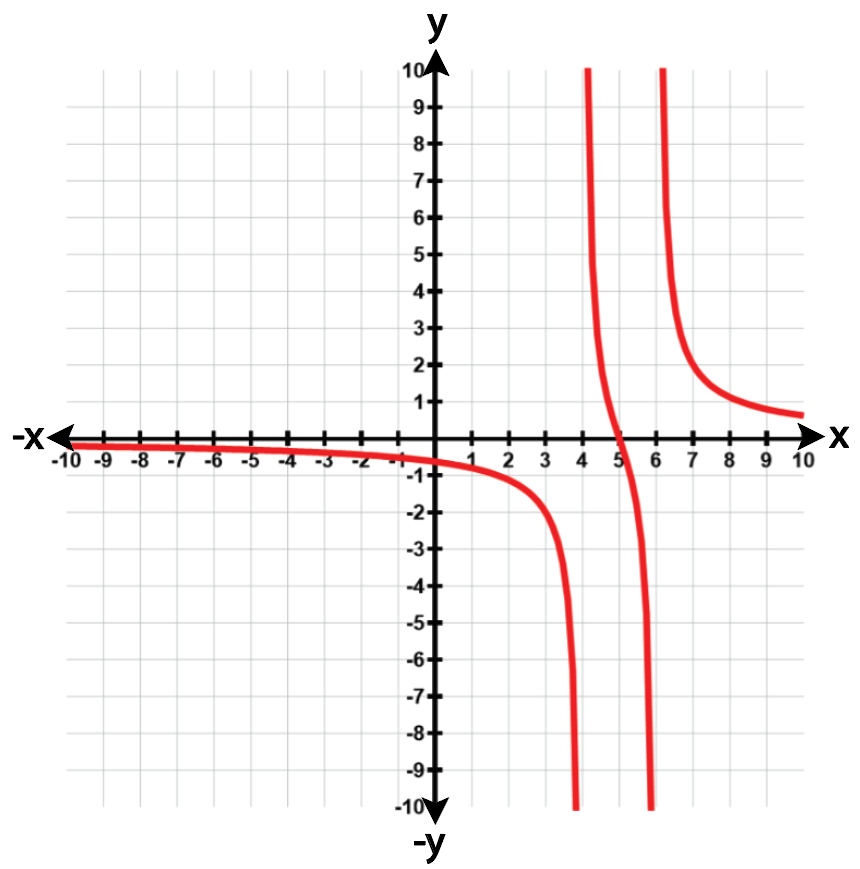
 Verified step by step guidance
Verified step by step guidance1
Identify the critical points of the function by setting the numerator and denominator equal to zero: 2(X-2) = 0 and (X-1)(X-3) = 0.
Solve for X to find the critical points: X = 2, X = 1, and X = 3.
Analyze the intervals created by these critical points: (-∞, 1), (1, 2), (2, 3), and (3, ∞).
Determine the sign of the function in each interval by selecting test points and substituting them into the inequality 2(X-2) / {(X-1)(X-3)} ≤ 0.
Use the graph to confirm the intervals where the function is less than or equal to zero and write the solution in interval notation.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
6mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Rational Functions
A rational function is a function represented by the ratio of two polynomials. In this case, the function is given by 2(X-2) / ((X-1)(X-3)). Understanding the behavior of rational functions, including their asymptotes and intercepts, is crucial for analyzing their graphs and solving inequalities.
Recommended video:

Intro to Rational Functions
Inequalities and Interval Notation
Inequalities express a relationship where one side is greater than or less than the other. Interval notation is a way to represent the solution set of an inequality using intervals, such as (a, b) for values between a and b, or [a, b] for including the endpoints. This notation is essential for clearly communicating the solution to the inequality presented.
Recommended video:

Interval Notation
Graph Analysis
Analyzing the graph of a function involves identifying key features such as intercepts, asymptotes, and regions where the function is positive or negative. For the given inequality, understanding where the graph is below the x-axis (i.e., where the function is less than or equal to zero) is necessary to determine the solution set in interval notation.
Recommended video:
Guided course

Graphs and Coordinates - Example
Related Videos
Related Practice