Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
10. Combinatorics & Probability
Combinatorics
Problem 89
Textbook Question
Textbook QuestionExercises 89–91 will help you prepare for the material covered in the next section. Evaluate n!/(n-r)! for n = 20 and r = 3
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Factorial
A factorial, denoted as n!, is the product of all positive integers from 1 to n. For example, 5! = 5 × 4 × 3 × 2 × 1 = 120. Factorials are fundamental in combinatorics, probability, and algebra, as they help in calculating permutations and combinations.
Recommended video:

Factorials
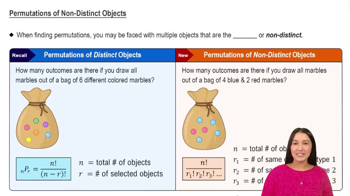
Permutations
Permutations refer to the different ways of arranging a set of items where the order matters. The formula for permutations of n items taken r at a time is given by n!/(n-r)!. This concept is crucial for solving problems involving arrangements and selections.
Recommended video:

Introduction to Permutations
Combination vs. Permutation
While both combinations and permutations deal with selecting items from a set, the key difference lies in order. Combinations do not consider order (e.g., choosing 3 fruits from 5), while permutations do (e.g., arranging 3 fruits in a line). Understanding this distinction is essential for correctly applying the factorial formula.
Recommended video:

Permutations vs. Combinations

 4:4m
4:4mWatch next
Master Fundamental Counting Principle with a bite sized video explanation from Callie
Start learning