Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
7. Systems of Equations & Matrices
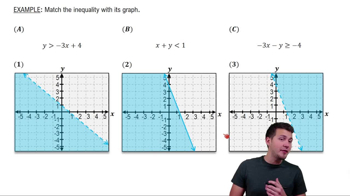
Graphing Systems of Inequalities
Problem 44
Textbook Question
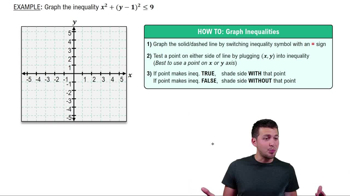
In Exercises 39–45, graph each inequality. y ≤ x^2 - 1
 Verified step by step guidance
Verified step by step guidance1
Step 1: Identify the equation of the boundary line. The inequality given is \( y \leq x^2 - 1 \). The boundary line is the equation \( y = x^2 - 1 \).
Step 2: Graph the boundary line. Since the inequality is \( \leq \), the boundary line \( y = x^2 - 1 \) will be a solid line. This is a parabola opening upwards with its vertex at the point (0, -1).
Step 3: Determine the region to shade. Since the inequality is \( y \leq x^2 - 1 \), shade the region below the parabola, as this represents all the points where \( y \) is less than or equal to \( x^2 - 1 \).
Step 4: Choose a test point to verify the shaded region. A common test point is (0,0). Substitute into the inequality: \( 0 \leq 0^2 - 1 \) simplifies to \( 0 \leq -1 \), which is false. Therefore, the region that does not include (0,0) is the correct shaded area.
Step 5: Label the graph. Clearly label the parabola and the shaded region to indicate the solution set of the inequality \( y \leq x^2 - 1 \).
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
5mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Inequalities
Inequalities are mathematical expressions that show the relationship between two values when they are not equal. They use symbols such as ≤ (less than or equal to), ≥ (greater than or equal to), < (less than), and > (greater than). Understanding how to interpret and manipulate inequalities is essential for graphing them accurately.
Recommended video:

Linear Inequalities
Quadratic Functions
A quadratic function is a polynomial function of degree two, typically expressed in the form f(x) = ax^2 + bx + c. The graph of a quadratic function is a parabola, which can open upwards or downwards depending on the sign of the coefficient 'a'. In the given inequality, y ≤ x^2 - 1, the function represents a parabola that opens upwards with its vertex at the point (0, -1).
Recommended video:

Solving Quadratic Equations Using The Quadratic Formula
Graphing Inequalities
Graphing inequalities involves shading a region of the coordinate plane to represent all the solutions that satisfy the inequality. For the inequality y ≤ x^2 - 1, you would first graph the parabola y = x^2 - 1 and then shade the area below the curve, indicating that all points in that region satisfy the inequality. Understanding how to represent these regions visually is crucial for solving and interpreting inequalities.
Recommended video:
Guided course

Linear Inequalities

 7:2m
7:2mWatch next
Master Linear Inequalities with a bite sized video explanation from Patrick Ford
Start learning