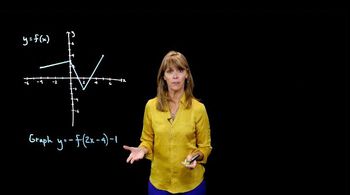Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
3. Functions
Transformations
Problem 52
Textbook Question
In Exercises 45-52, use the graph of y = f(x) to graph each function g. g(x)=2f(x-1)
 Verified step by step guidance
Verified step by step guidance1
Identify the transformations applied to the function \( f(x) \) to obtain \( g(x) = 2f(x-1) \).
Recognize that \( f(x-1) \) represents a horizontal shift of the graph of \( f(x) \) to the right by 1 unit.
Understand that multiplying \( f(x-1) \) by 2, as in \( 2f(x-1) \), results in a vertical stretch of the graph by a factor of 2.
Start by shifting the entire graph of \( f(x) \) to the right by 1 unit to account for the \( (x-1) \) term.
After shifting, stretch the graph vertically by multiplying the \( y \)-values of the shifted graph by 2 to complete the transformation.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Function Transformation
Function transformation refers to the changes made to the graph of a function based on modifications to its equation. Common transformations include vertical and horizontal shifts, stretches, and reflections. In the case of g(x) = 2f(x-1), the function is horizontally shifted to the right by 1 unit and vertically stretched by a factor of 2.
Recommended video:

Domain & Range of Transformed Functions
Horizontal Shift
A horizontal shift occurs when the input of a function is altered, resulting in the graph moving left or right. For g(x) = 2f(x-1), the 'x-1' indicates a shift to the right by 1 unit. This means that every point on the graph of f(x) will be moved one unit to the right to create the graph of g(x).
Recommended video:

Shifts of Functions
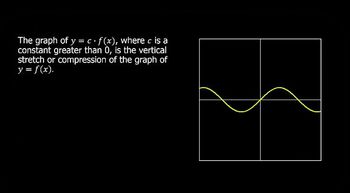
Vertical Stretch
A vertical stretch occurs when the output of a function is multiplied by a factor greater than 1, which increases the distance of points from the x-axis. In g(x) = 2f(x-1), the factor of 2 indicates that the graph of f(x) will be stretched vertically, making it twice as tall. This transformation affects the y-values of the function, amplifying the graph's height.
Recommended video:

Stretches & Shrinks of Functions

 5:25m
5:25mWatch next
Master Intro to Transformations with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice