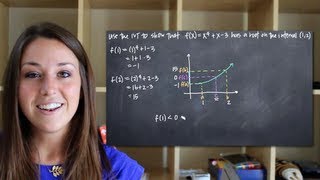In Exercises 33–40, use the Intermediate Value Theorem to show that each polynomial has a real zero between the given integers. f(x)=3x^3−8x^2+x+2; between 2 and 3

Key Concepts

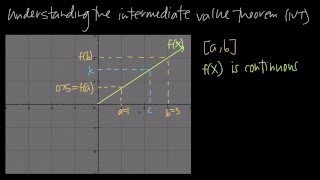
Intermediate Value Theorem

The Intermediate Value Theorem states that if a function is continuous on a closed interval [a, b] and takes on different signs at the endpoints, then there exists at least one c in (a, b) such that f(c) = 0. This theorem is crucial for proving the existence of real zeros in polynomial functions.

Polynomial Functions

A polynomial function is a mathematical expression involving a sum of powers in one or more variables multiplied by coefficients. In this case, f(x) = 3x^3 - 8x^2 + x + 2 is a cubic polynomial, which is continuous and differentiable everywhere, making it suitable for applying the Intermediate Value Theorem.

Sign Change

A sign change occurs when the value of a function changes from positive to negative or vice versa. To apply the Intermediate Value Theorem, we evaluate the polynomial at the endpoints of the interval [2, 3]. If f(2) and f(3) have opposite signs, it confirms that there is at least one real zero in that interval.