Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
4. Polynomial Functions
Dividing Polynomials
Problem 53b
Textbook Question
In Exercises 53–54, write a polynomial that represents the length of each rectangle.
Transcription: The area of the rectangle is 0.5x^3 - 0.3x^2 + 0.22x + 0.06 square units and its width is x + 0.2 units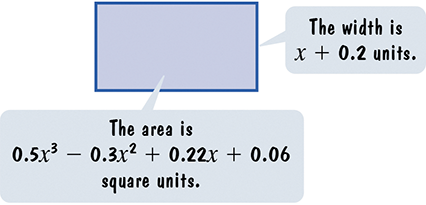
 Verified step by step guidance
Verified step by step guidance1
Identify the formula for the area of a rectangle, which is given by \( \text{Area} = \text{Length} \times \text{Width} \).
Given the area of the rectangle as \( 0.5x^3 - 0.3x^2 + 0.22x + 0.06 \) and the width as \( x + 0.2 \), set up the equation: \( 0.5x^3 - 0.3x^2 + 0.22x + 0.06 = \text{Length} \times (x + 0.2) \).
To find the length, divide the polynomial representing the area by the polynomial representing the width: \( \text{Length} = \frac{0.5x^3 - 0.3x^2 + 0.22x + 0.06}{x + 0.2} \).
Perform polynomial long division or synthetic division to divide \( 0.5x^3 - 0.3x^2 + 0.22x + 0.06 \) by \( x + 0.2 \).
The quotient obtained from the division will be the polynomial that represents the length of the rectangle.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
5mPlay a video:
Was this helpful?
Related Videos
Related Practice

