Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
5. Rational Functions
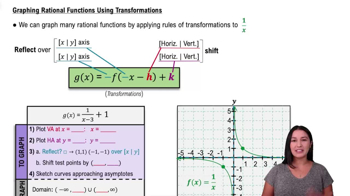
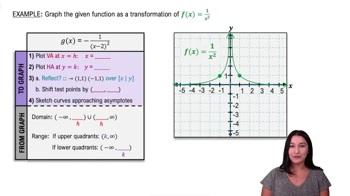
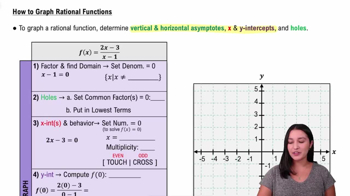
Graphing Rational Functions
Problem 2
Textbook Question
Provide a short answer to each question. What is the domain of the function ƒ(x)=1/x^2? What is its range?
 Verified step by step guidance
Verified step by step guidance1
<Step 1: Understand the function. The function given is \( f(x) = \frac{1}{x^2} \).>
<Step 2: Determine the domain. The domain of a function is the set of all possible input values (x-values) that will not make the function undefined.>
<Step 3: Identify restrictions for the domain. Since the function has \( x^2 \) in the denominator, it cannot be zero. Therefore, \( x \neq 0 \).>
<Step 4: State the domain. The domain of \( f(x) = \frac{1}{x^2} \) is all real numbers except zero, which can be written as \( (-\infty, 0) \cup (0, \infty) \).>
<Step 5: Determine the range. Since \( x^2 \) is always positive for any real number \( x \neq 0 \), \( \frac{1}{x^2} \) is always positive. Thus, the range is \( (0, \infty) \).>
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
5mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Domain of a Function
The domain of a function refers to the set of all possible input values (x-values) for which the function is defined. For the function ƒ(x) = 1/x², the domain excludes any values that make the denominator zero, which in this case is x = 0. Therefore, the domain is all real numbers except zero, expressed as (-∞, 0) ∪ (0, ∞).
Recommended video:

Domain Restrictions of Composed Functions
Range of a Function
The range of a function is the set of all possible output values (y-values) that the function can produce. For ƒ(x) = 1/x², as x approaches zero from either side, the function approaches infinity, and as x moves away from zero, the function approaches zero but never reaches it. Thus, the range is all positive real numbers, expressed as (0, ∞).
Recommended video:

Domain & Range of Transformed Functions
Vertical Asymptote
A vertical asymptote is a line that a graph approaches but never touches or crosses, indicating where a function's value becomes unbounded. In the case of ƒ(x) = 1/x², there is a vertical asymptote at x = 0, which signifies that as x approaches zero, the function's value increases without bound, reinforcing the understanding of the domain and range.
Recommended video:

Determining Vertical Asymptotes

 5:31m
5:31mWatch next
Master Graphing Rational Functions Using Transformations with a bite sized video explanation from Callie
Start learningRelated Videos
Related Practice